Coordinate descent on the orthogonal group for recurrent neural network training
Paper and Code
Jul 30, 2021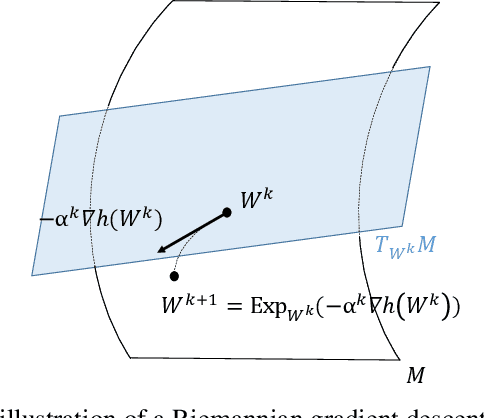

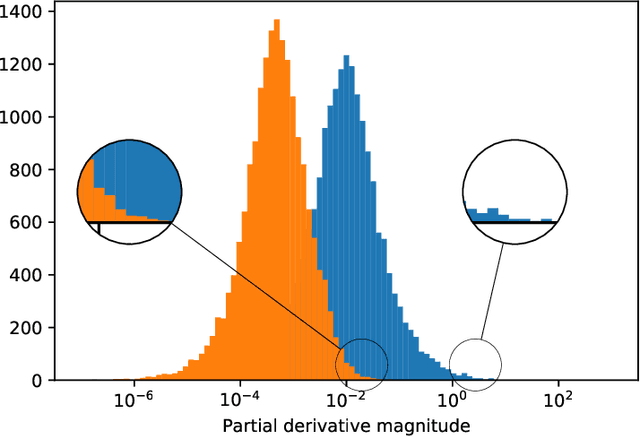
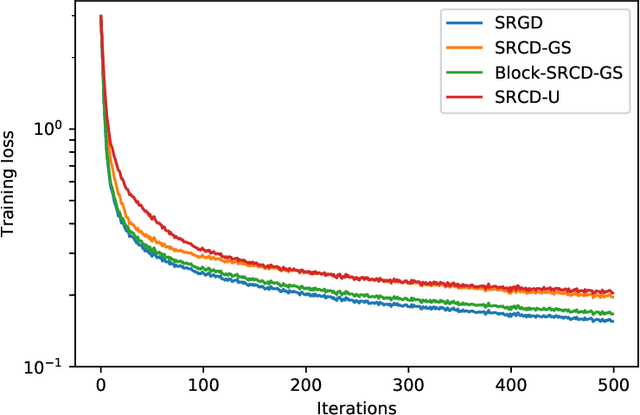
We propose to use stochastic Riemannian coordinate descent on the orthogonal group for recurrent neural network training. The algorithm rotates successively two columns of the recurrent matrix, an operation that can be efficiently implemented as a multiplication by a Givens matrix. In the case when the coordinate is selected uniformly at random at each iteration, we prove the convergence of the proposed algorithm under standard assumptions on the loss function, stepsize and minibatch noise. In addition, we numerically demonstrate that the Riemannian gradient in recurrent neural network training has an approximately sparse structure. Leveraging this observation, we propose a faster variant of the proposed algorithm that relies on the Gauss-Southwell rule. Experiments on a benchmark recurrent neural network training problem are presented to demonstrate the effectiveness of the proposed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge