Testing GPT-4 with Wolfram Alpha and Code Interpreter plug-ins on math and science problems

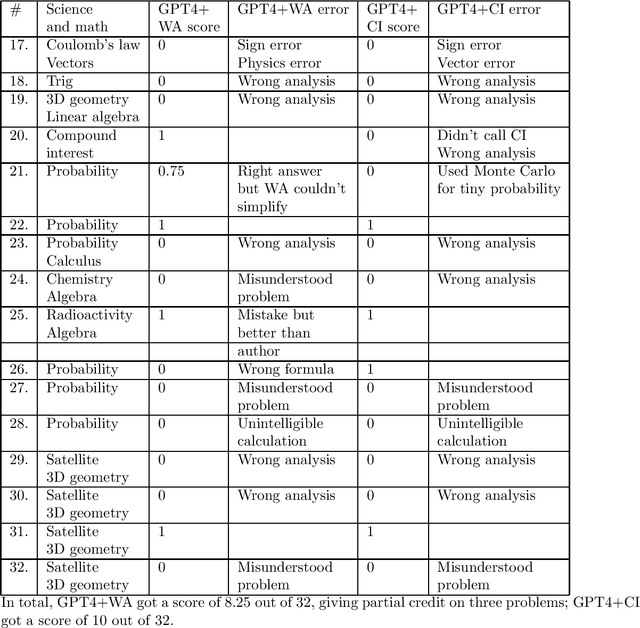
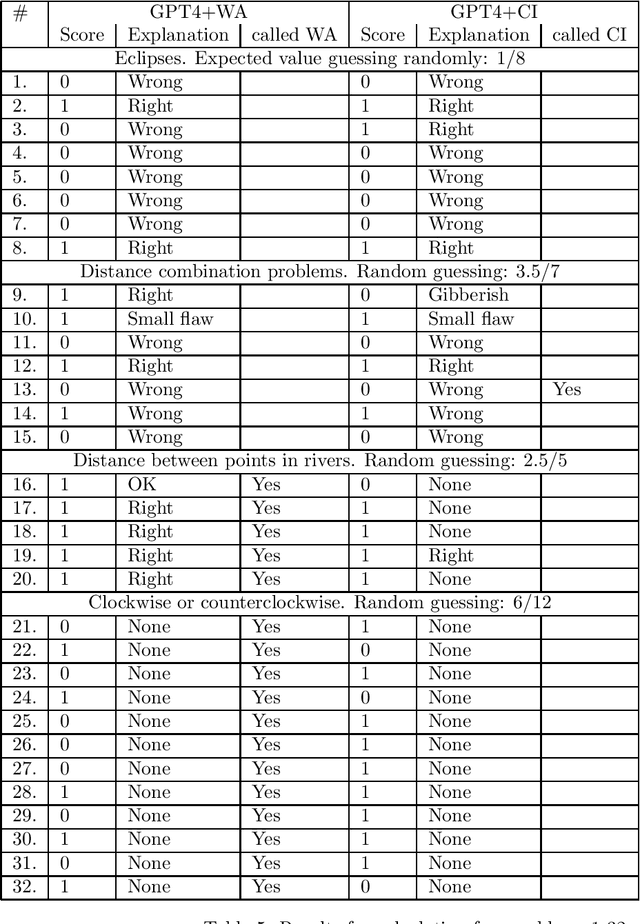
This report describes a test of the large language model GPT-4 with the Wolfram Alpha and the Code Interpreter plug-ins on 105 original problems in science and math, at the high school and college levels, carried out in June-August 2023. Our tests suggest that the plug-ins significantly enhance GPT's ability to solve these problems. Having said that, there are still often "interface" failures; that is, GPT often has trouble formulating problems in a way that elicits useful answers from the plug-ins. Fixing these interface failures seems like a central challenge in making GPT a reliable tool for college-level calculation problems.

Benchmarks for Automated Commonsense Reasoning: A Survey

More than one hundred benchmarks have been developed to test the commonsense knowledge and commonsense reasoning abilities of artificial intelligence (AI) systems. However, these benchmarks are often flawed and many aspects of common sense remain untested. Consequently, we do not currently have any reliable way of measuring to what extent existing AI systems have achieved these abilities. This paper surveys the development and uses of AI commonsense benchmarks. We discuss the nature of common sense; the role of common sense in AI; the goals served by constructing commonsense benchmarks; and desirable features of commonsense benchmarks. We analyze the common flaws in benchmarks, and we argue that it is worthwhile to invest the work needed ensure that benchmark examples are consistently high quality. We survey the various methods of constructing commonsense benchmarks. We enumerate 139 commonsense benchmarks that have been developed: 102 text-based, 18 image-based, 12 video based, and 7 simulated physical environments. We discuss the gaps in the existing benchmarks and aspects of commonsense reasoning that are not addressed in any existing benchmark. We conclude with a number of recommendations for future development of commonsense AI benchmarks.

Mathematics, word problems, common sense, and artificial intelligence

The paper discusses the capacities and limitations of current artificial intelligence (AI) technology to solve word problems that combine elementary knowledge with commonsense reasoning. No existing AI systems can solve these reliably. We review three approaches that have been developed, using AI natural language technology: outputting the answer directly, outputting a computer program that solves the problem, and outputting a formalized representation that can be input to an automated theorem verifier. We review some benchmarks that have been developed to evaluate these systems and some experimental studies. We discuss the limitations of the existing technology at solving these kinds of problems. We argue that it is not clear whether these kinds of limitations will be important in developing AI technology for pure mathematical research, but that they will be important in applications of mathematics, and may well be important in developing programs capable of reading and understanding mathematical content written by humans.

Limits of an AI program for solving college math problems

Drori et al. (2022) report that "A neural network solves, explains, and generates university math problems by program synthesis and few-shot learning at human level ... [It] automatically answers 81\% of university-level mathematics problems." The system they describe is indeed impressive; however, the above description is very much overstated. The work of solving the problems is done, not by a neural network, but by the symbolic algebra package Sympy. Problems of various formats are excluded from consideration. The so-called "explanations" are just rewordings of lines of code. Answers are marked as correct that are not in the form specified in the problem. Most seriously, it seems that in many cases the system uses the correct answer given in the test corpus to guide its path to solving the problem.

A very preliminary analysis of DALL-E 2

The DALL-E 2 system generates original synthetic images corresponding to an input text as caption. We report here on the outcome of fourteen tests of this system designed to assess its common sense, reasoning and ability to understand complex texts. All of our prompts were intentionally much more challenging than the typical ones that have been showcased in recent weeks. Nevertheless, for 5 out of the 14 prompts, at least one of the ten images fully satisfied our requests. On the other hand, on no prompt did all of the ten images satisfy our requests.

Pragmatic constraints and pronoun reference disambiguation: the possible and the impossible

Pronoun disambiguation in understanding text and discourse often requires the application of both general pragmatic knowledge and context-specific information. In AI and linguistics research, this has mostly been studied in cases where the referent is explicitly stated in the preceding text nearby. However, pronouns in natural text often refer to entities, collections, or events that are only implicitly mentioned previously; in those cases the need to use pragmatic knowledge to disambiguate becomes much more acute and the characterization of the knowledge becomes much more difficult. Extended literary texts at times employ both extremely complex patterns of reference and extremely rich and subtle forms of knowledge. Indeed, it is occasionally possible to have a pronoun that is far separated from its referent in a text. In the opposite direction, pronoun use is affected by considerations of focus of attention and by formal constraints such as a preference for parallel syntactic structures; these can be so strong that no pragmatic knowledge suffices to overrule them.

Physical Reasoning in an Open World

Most work on physical reasoning, both in artificial intelligence and in cognitive science, has focused on closed-world reasoning, in which it is assumed that the problem specification specifies all relevant objects and substance, all their relations in an initial situation, and all exogenous events. However, in many situations, it is important to do open-world reasoning; that is, making valid conclusions from very incomplete information. We have implemented in Prolog an open-world reasoner for a toy microworld of containers that can be loaded, unloaded, sealed, unsealed, carried, and dumped.

The Defeat of the Winograd Schema Challenge

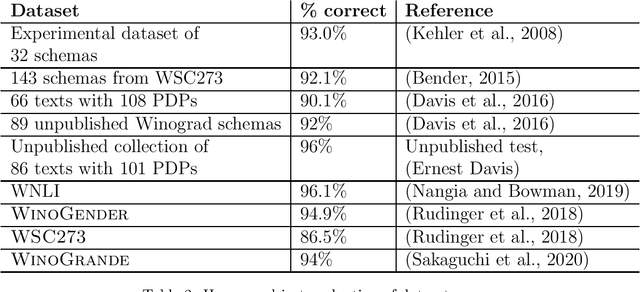
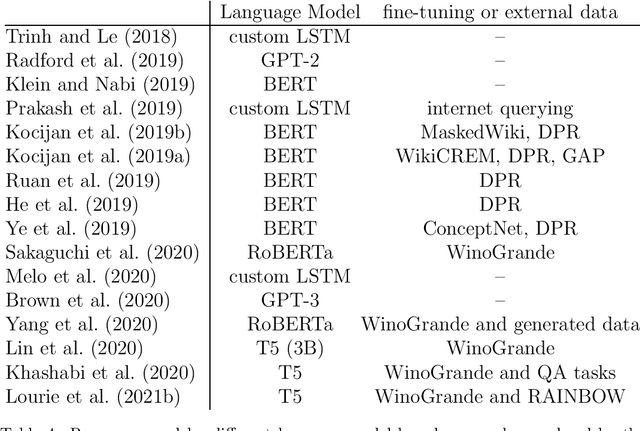
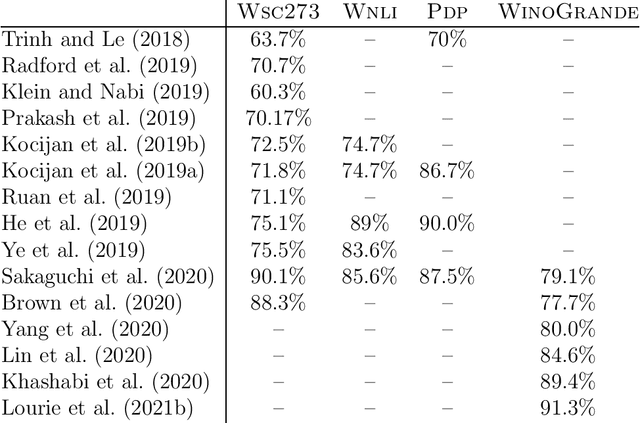
The Winograd Schema Challenge -- a set of twin sentences involving pronoun reference disambiguation that seem to require the use of commonsense knowledge -- was proposed by Hector Levesque in 2011. By 2019, a number of AI systems, based on large pre-trained transformer-based language models and fine-tuned on these kinds of problems, achieved better than 90% accuracy. In this paper, we review the history of the Winograd Schema Challenge and assess its significance.

Deep Learning and Mathematical Intuition: A Review of (Davies et al. 2021)

A recent paper by Davies et al (2021) describes how deep learning (DL) technology was used to find plausible hypotheses that have led to two original mathematical results: one in knot theory, one in representation theory. I argue here that the significance and novelty of this application of DL technology to mathematics is significantly overstated in the paper under review and has been wildly overstated in some of the accounts in the popular science press. In the knot theory result, the role of DL was small, and a conventional statistical analysis would probably have sufficed. In the representation theory result, the role of DL is much larger; however, it is not very different in kind from what has been done in experimental mathematics for decades. Moreover, it is not clear whether the distinctive features of DL that make it useful here will apply across a wide range of mathematical problems. Finally, I argue that the DL here "guides human intuition" is unhelpful and misleading; what the DL does primarily does is to mark many possible conjectures as false and a few others as possibly worthy of study. Certainly the representation theory result represents an original and interesting application of DL to mathematical research, but its larger significance is uncertain.

A Flawed Dataset for Symbolic Equation Verification

Arabshahi, Singh, and Anandkumar (2018) propose a method for creating a dataset of symbolic mathematical equations for the tasks of symbolic equation verification and equation completion. Unfortunately, a dataset constructed using the method they propose will suffer from two serious flaws. First, the class of true equations that the procedure can generate will be very limited. Second, because true and false equations are generated in completely different ways, there are likely to be artifactual features that allow easy discrimination. Moreover, over the class of equations they consider, there is an extremely simple probabilistic procedure that solves the problem of equation verification with extremely high reliability. The usefulness of this problem in general as a testbed for AI systems is therefore doubtful.