GP-ALPS: Automatic Latent Process Selection for Multi-Output Gaussian Process Models

A simple and widely adopted approach to extend Gaussian processes (GPs) to multiple outputs is to model each output as a linear combination of a collection of shared, unobserved latent GPs. An issue with this approach is choosing the number of latent processes and their kernels. These choices are typically done manually, which can be time consuming and prone to human biases. We propose Gaussian Process Automatic Latent Process Selection (GP-ALPS), which automatically chooses the latent processes by turning off those that do not meaningfully contribute to explaining the data. We develop a variational inference scheme, assess the quality of the variational posterior by comparing it against the gold standard MCMC, and demonstrate the suitability of GP-ALPS in a set of preliminary experiments.

Scalable Exact Inference in Multi-Output Gaussian Processes

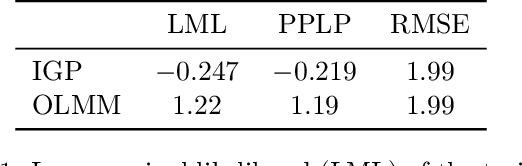
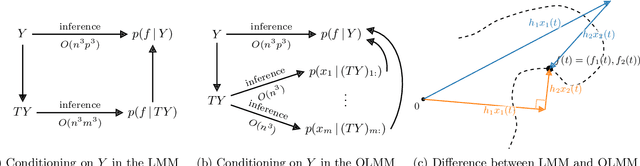
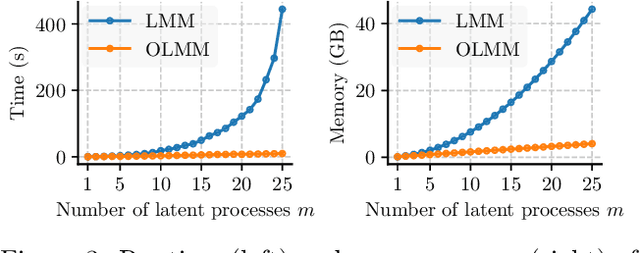
Multi-output Gaussian processes (MOGPs) leverage the flexibility and interpretability of GPs while capturing structure across outputs, which is desirable, for example, in spatio-temporal modelling. The key problem with MOGPs is the cubic computational scaling in the number of both inputs (e.g., time points or locations), n, and outputs, p. Current methods reduce this to O(n^3 m^3), where m < p is the desired degrees of freedom. This computational cost, however, is still prohibitive in many applications. To address this limitation, we present the Orthogonal Linear Mixing Model (OLMM), an MOGP in which exact inference scales linearly in m: O(n^3 m). This advance opens up a wide range of real-world tasks and can be combined with existing GP approximations in a plug-and-play way as demonstrated in the paper. Additionally, the paper organises the existing disparate literature on MOGP models into a simple taxonomy called the Mixing Model Hierarchy (MMH).