Scalable Exact Inference in Multi-Output Gaussian Processes
Paper and Code
Nov 14, 2019
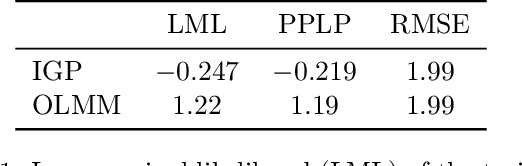
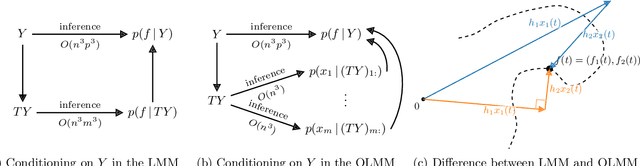
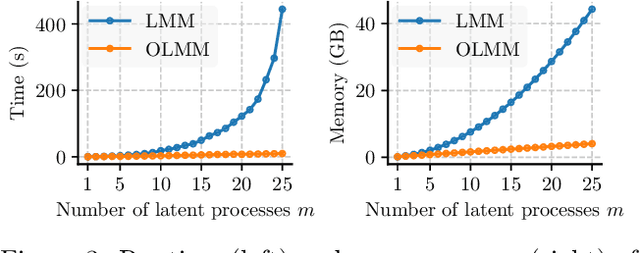
Multi-output Gaussian processes (MOGPs) leverage the flexibility and interpretability of GPs while capturing structure across outputs, which is desirable, for example, in spatio-temporal modelling. The key problem with MOGPs is the cubic computational scaling in the number of both inputs (e.g., time points or locations), n, and outputs, p. Current methods reduce this to O(n^3 m^3), where m < p is the desired degrees of freedom. This computational cost, however, is still prohibitive in many applications. To address this limitation, we present the Orthogonal Linear Mixing Model (OLMM), an MOGP in which exact inference scales linearly in m: O(n^3 m). This advance opens up a wide range of real-world tasks and can be combined with existing GP approximations in a plug-and-play way as demonstrated in the paper. Additionally, the paper organises the existing disparate literature on MOGP models into a simple taxonomy called the Mixing Model Hierarchy (MMH).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge