Relational Algebra and Calculus with SQL Null Values

The logic of nulls in databases has been subject of investigation since their introduction in Codd's Relational Model, which is the foundation of the SQL standard. We show a logical characterisation of a first-order fragment of SQL with null values, by first focussing on a simple extension with null values of standard relational algebra, which captures exactly the SQL fragment, and then proposing two different domain relational calculi, in which the null value is a term of the language but it does not appear as an element of the semantic interpretation domain of the logics. In one calculus, a relation can be seen as a set of partial tuples, while in the other (equivalent) calculus, a relation is horizontally decomposed as a set of relations each one holding regular total tuples. We extend Codd's theorem by proving the equivalence of the relational algebra with both domain relational calculi in presence of SQL null values.

A Decidable Very Expressive Description Logic for Databases (Extended Version)

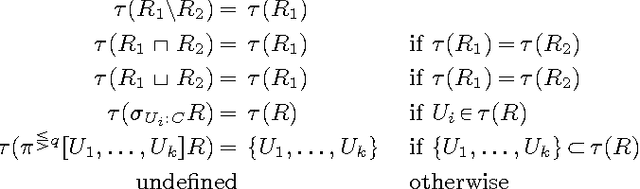
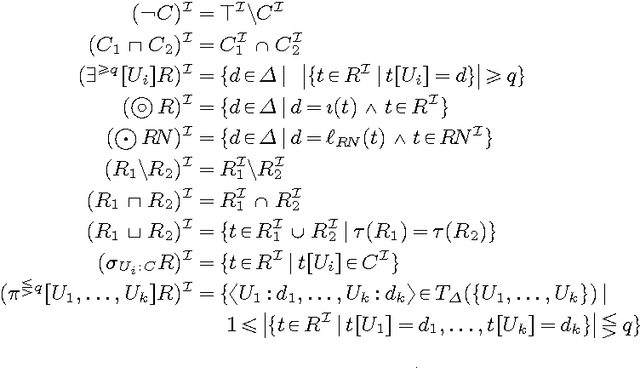
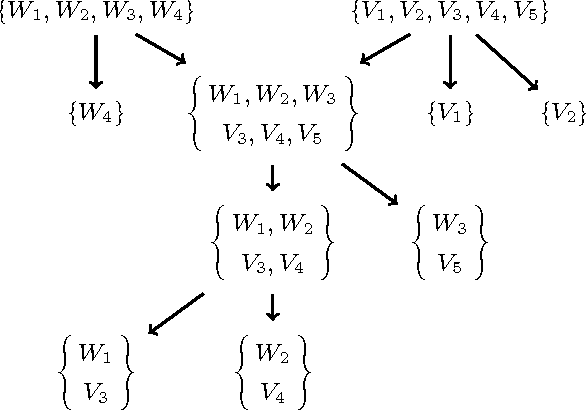
We introduce $\mathcal{DLR}^+$, an extension of the n-ary propositionally closed description logic $\mathcal{DLR}$ to deal with attribute-labelled tuples (generalising the positional notation), projections of relations, and global and local objectification of relations, able to express inclusion, functional, key, and external uniqueness dependencies. The logic is equipped with both TBox and ABox axioms. We show how a simple syntactic restriction on the appearance of projections sharing common attributes in a $\mathcal{DLR}^+$ knowledge base makes reasoning in the language decidable with the same computational complexity as $\mathcal{DLR}$. The obtained $\mathcal{DLR}^\pm$ n-ary description logic is able to encode more thoroughly conceptual data models such as EER, UML, and ORM.

Extending DLR with Labelled Tuples, Projections, Functional Dependencies and Objectification (full version)

We introduce an extension of the n-ary description logic DLR to deal with attribute-labelled tuples (generalising the positional notation), with arbitrary projections of relations (inclusion dependencies), generic functional dependencies and with global and local objectification (reifying relations or their projections). We show how a simple syntactic condition on the appearance of projections and functional dependencies in a knowledge base makes the language decidable without increasing the computational complexity of the basic DLR language.

Data complexity of answering conjunctive queries over SHIQ knowledge bases

An algorithm for answering conjunctive queries over SHIQ knowledge bases that is coNP in data complexity is given. The algorithm is based on the tableau algorithm for reasoning with individuals in SHIQ. The blocking conditions of the tableau are weakened in such a way that the set of models the modified algorithm yields suffices to check query entailment. The modified blocking conditions are based on the ones proposed by Levy and Rousset for reasoning with Horn Rules in the description logic ALCNR.