A Decidable Very Expressive Description Logic for Databases (Extended Version)
Paper and Code
Jul 25, 2017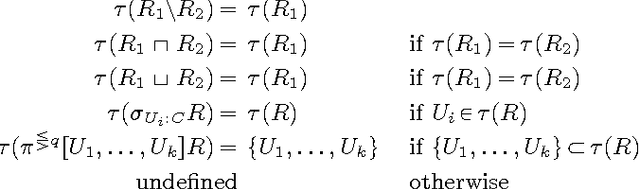
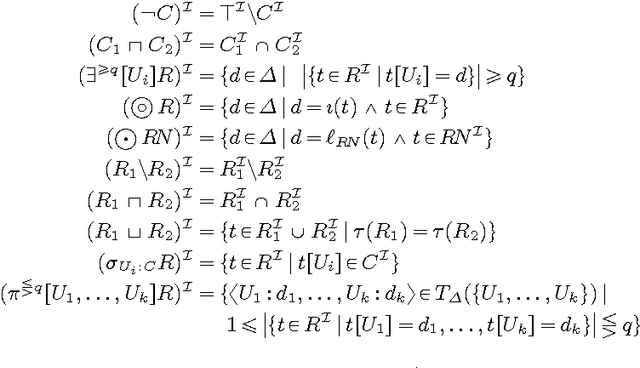
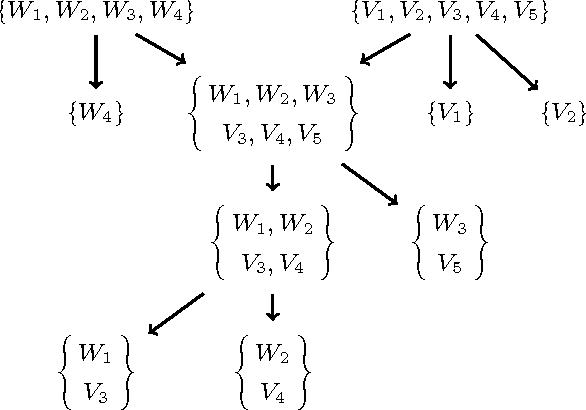

We introduce $\mathcal{DLR}^+$, an extension of the n-ary propositionally closed description logic $\mathcal{DLR}$ to deal with attribute-labelled tuples (generalising the positional notation), projections of relations, and global and local objectification of relations, able to express inclusion, functional, key, and external uniqueness dependencies. The logic is equipped with both TBox and ABox axioms. We show how a simple syntactic restriction on the appearance of projections sharing common attributes in a $\mathcal{DLR}^+$ knowledge base makes reasoning in the language decidable with the same computational complexity as $\mathcal{DLR}$. The obtained $\mathcal{DLR}^\pm$ n-ary description logic is able to encode more thoroughly conceptual data models such as EER, UML, and ORM.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge