Estimating the Robustness Radius for Randomized Smoothing with 100$\times$ Sample Efficiency

Randomized smoothing (RS) has successfully been used to improve the robustness of predictions for deep neural networks (DNNs) by adding random noise to create multiple variations of an input, followed by deciding the consensus. To understand if an RS-enabled DNN is effective in the sampled input domains, it is mandatory to sample data points within the operational design domain, acquire the point-wise certificate regarding robustness radius, and compare it with pre-defined acceptance criteria. Consequently, ensuring that a point-wise robustness certificate for any given data point is obtained relatively cost-effectively is crucial. This work demonstrates that reducing the number of samples by one or two orders of magnitude can still enable the computation of a slightly smaller robustness radius (commonly ~20% radius reduction) with the same confidence. We provide the mathematical foundation for explaining the phenomenon while experimentally showing promising results on the standard CIFAR-10 and ImageNet datasets.

Prioritizing Corners in OoD Detectors via Symbolic String Manipulation

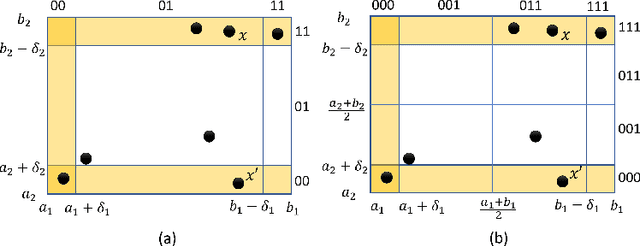
For safety assurance of deep neural networks (DNNs), out-of-distribution (OoD) monitoring techniques are essential as they filter spurious input that is distant from the training dataset. This paper studies the problem of systematically testing OoD monitors to avoid cases where an input data point is tested as in-distribution by the monitor, but the DNN produces spurious output predictions. We consider the definition of "in-distribution" characterized in the feature space by a union of hyperrectangles learned from the training dataset. Thus the testing is reduced to finding corners in hyperrectangles distant from the available training data in the feature space. Concretely, we encode the abstract location of every data point as a finite-length binary string, and the union of all binary strings is stored compactly using binary decision diagrams (BDDs). We demonstrate how to use BDDs to symbolically extract corners distant from all data points within the training set. Apart from test case generation, we explain how to use the proposed corners to fine-tune the DNN to ensure that it does not predict overly confidently. The result is evaluated over examples such as number and traffic sign recognition.

Unaligned but Safe -- Formally Compensating Performance Limitations for Imprecise 2D Object Detection

In this paper, we consider the imperfection within machine learning-based 2D object detection and its impact on safety. We address a special sub-type of performance limitations: the prediction bounding box cannot be perfectly aligned with the ground truth, but the computed Intersection-over-Union metric is always larger than a given threshold. Under such type of performance limitation, we formally prove the minimum required bounding box enlargement factor to cover the ground truth. We then demonstrate that the factor can be mathematically adjusted to a smaller value, provided that the motion planner takes a fixed-length buffer in making its decisions. Finally, observing the difference between an empirically measured enlargement factor and our formally derived worst-case enlargement factor offers an interesting connection between the quantitative evidence (demonstrated by statistics) and the qualitative evidence (demonstrated by worst-case analysis).