Unaligned but Safe -- Formally Compensating Performance Limitations for Imprecise 2D Object Detection

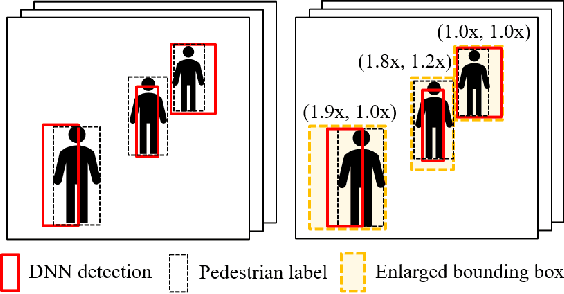
In this paper, we consider the imperfection within machine learning-based 2D object detection and its impact on safety. We address a special sub-type of performance limitations: the prediction bounding box cannot be perfectly aligned with the ground truth, but the computed Intersection-over-Union metric is always larger than a given threshold. Under such type of performance limitation, we formally prove the minimum required bounding box enlargement factor to cover the ground truth. We then demonstrate that the factor can be mathematically adjusted to a smaller value, provided that the motion planner takes a fixed-length buffer in making its decisions. Finally, observing the difference between an empirically measured enlargement factor and our formally derived worst-case enlargement factor offers an interesting connection between the quantitative evidence (demonstrated by statistics) and the qualitative evidence (demonstrated by worst-case analysis).

Logically Sound Arguments for the Effectiveness of ML Safety Measures

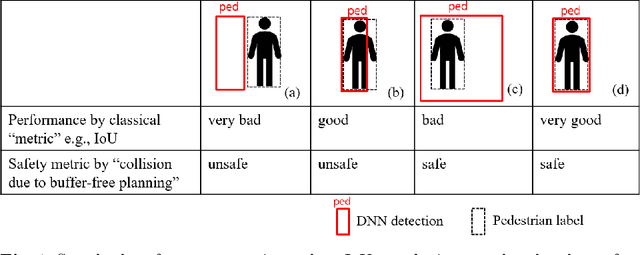
We investigate the issues of achieving sufficient rigor in the arguments for the safety of machine learning functions. By considering the known weaknesses of DNN-based 2D bounding box detection algorithms, we sharpen the metric of imprecise pedestrian localization by associating it with the safety goal. The sharpening leads to introducing a conservative post-processor after the standard non-max-suppression as a counter-measure. We then propose a semi-formal assurance case for arguing the effectiveness of the post-processor, which is further translated into formal proof obligations for demonstrating the soundness of the arguments. Applying theorem proving not only discovers the need to introduce missing claims and mathematical concepts but also reveals the limitation of Dempster-Shafer's rules used in semi-formal argumentation.