Forecasting the Intra-Day Spread Densities of Electricity Prices

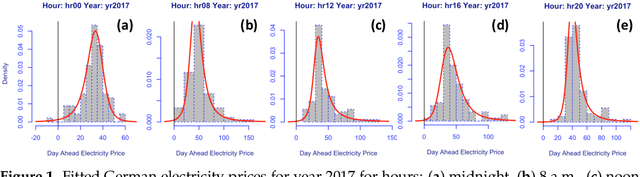
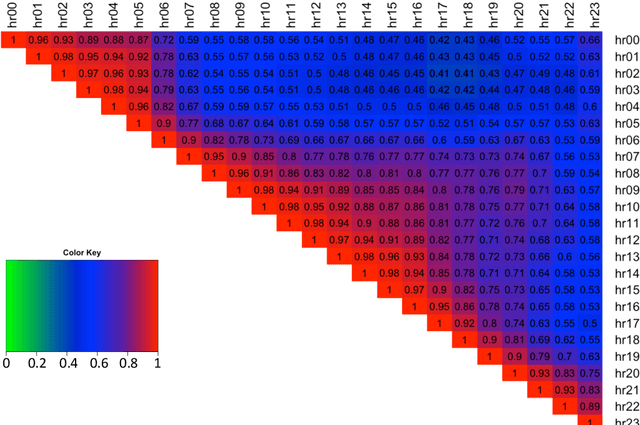
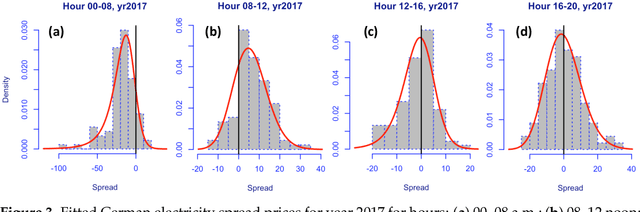
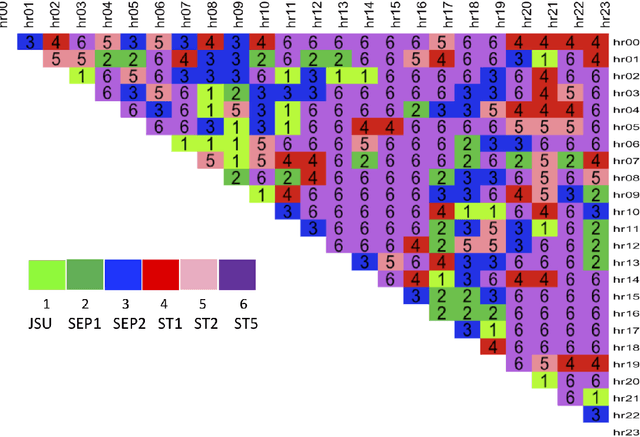
Intra-day price spreads are of interest to electricity traders, storage and electric vehicle operators. This paper formulates dynamic density functions, based upon skewed-t and similar representations, to model and forecast the German electricity price spreads between different hours of the day, as revealed in the day-ahead auctions. The four specifications of the density functions are dynamic and conditional upon exogenous drivers, thereby permitting the location, scale and shape parameters of the densities to respond hourly to such factors as weather and demand forecasts. The best fitting and forecasting specifications for each spread are selected based on the Pinball Loss function, following the closed-form analytical solutions of the cumulative distribution functions.

Estimating Dynamic Conditional Spread Densities to Optimise Daily Storage Trading of Electricity

This paper formulates dynamic density functions, based upon skewed-t and similar representations, to model and forecast electricity price spreads between different hours of the day. This supports an optimal day ahead storage and discharge schedule, and thereby facilitates a bidding strategy for a merchant arbitrage facility into the day-ahead auctions for wholesale electricity. The four latent moments of the density functions are dynamic and conditional upon exogenous drivers, thereby permitting the mean, variance, skewness and kurtosis of the densities to respond hourly to such factors as weather and demand forecasts. The best specification for each spread is selected based on the Pinball Loss function, following the closed form analytical solutions of the cumulative density functions. Those analytical properties also allow the calculation of risk associated with the spread arbitrages. From these spread densities, the optimal daily operation of a battery storage facility is determined.

RLOC: Neurobiologically Inspired Hierarchical Reinforcement Learning Algorithm for Continuous Control of Nonlinear Dynamical Systems

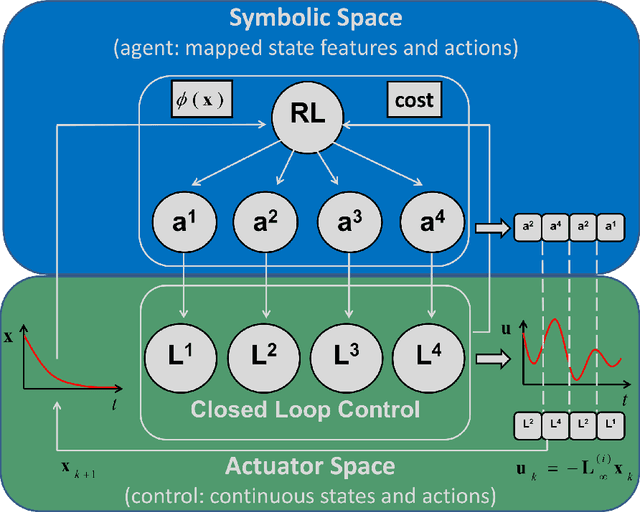
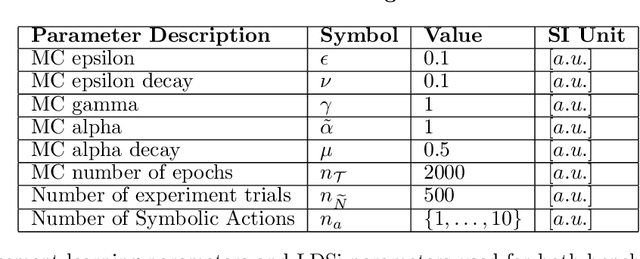
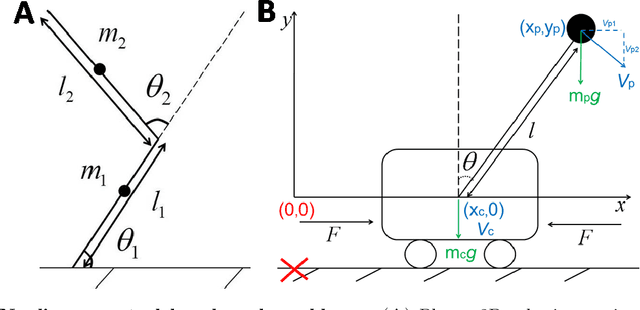
Nonlinear optimal control problems are often solved with numerical methods that require knowledge of system's dynamics which may be difficult to infer, and that carry a large computational cost associated with iterative calculations. We present a novel neurobiologically inspired hierarchical learning framework, Reinforcement Learning Optimal Control, which operates on two levels of abstraction and utilises a reduced number of controllers to solve nonlinear systems with unknown dynamics in continuous state and action spaces. Our approach is inspired by research at two levels of abstraction: first, at the level of limb coordination human behaviour is explained by linear optimal feedback control theory. Second, in cognitive tasks involving learning symbolic level action selection, humans learn such problems using model-free and model-based reinforcement learning algorithms. We propose that combining these two levels of abstraction leads to a fast global solution of nonlinear control problems using reduced number of controllers. Our framework learns the local task dynamics from naive experience and forms locally optimal infinite horizon Linear Quadratic Regulators which produce continuous low-level control. A top-level reinforcement learner uses the controllers as actions and learns how to best combine them in state space while maximising a long-term reward. A single optimal control objective function drives high-level symbolic learning by providing training signals on desirability of each selected controller. We show that a small number of locally optimal linear controllers are able to solve global nonlinear control problems with unknown dynamics when combined with a reinforcement learner in this hierarchical framework. Our algorithm competes in terms of computational cost and solution quality with sophisticated control algorithms and we illustrate this with solutions to benchmark problems.