RLOC: Neurobiologically Inspired Hierarchical Reinforcement Learning Algorithm for Continuous Control of Nonlinear Dynamical Systems
Paper and Code
Mar 07, 2019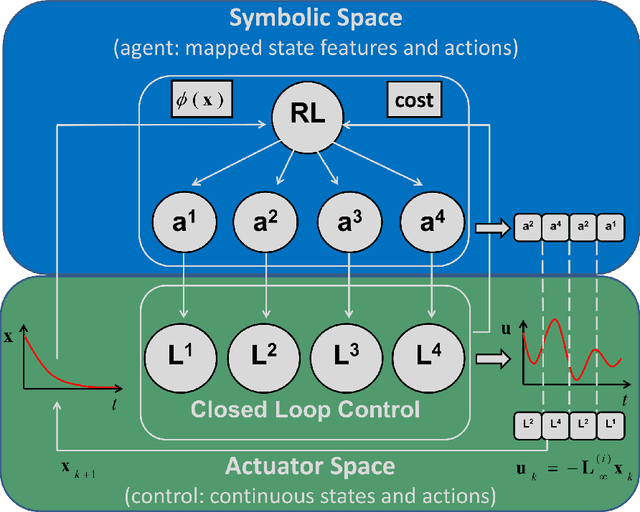

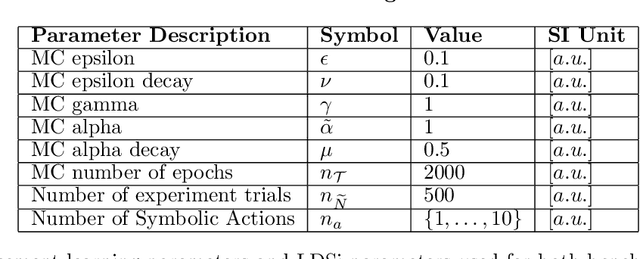
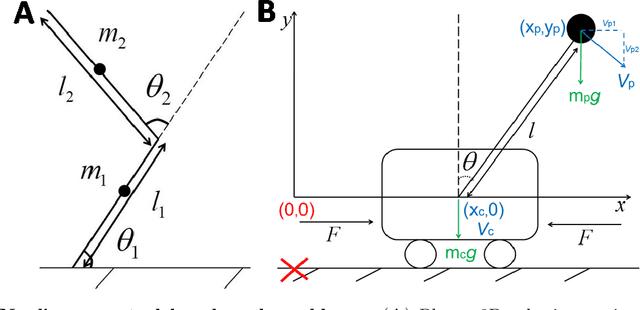
Nonlinear optimal control problems are often solved with numerical methods that require knowledge of system's dynamics which may be difficult to infer, and that carry a large computational cost associated with iterative calculations. We present a novel neurobiologically inspired hierarchical learning framework, Reinforcement Learning Optimal Control, which operates on two levels of abstraction and utilises a reduced number of controllers to solve nonlinear systems with unknown dynamics in continuous state and action spaces. Our approach is inspired by research at two levels of abstraction: first, at the level of limb coordination human behaviour is explained by linear optimal feedback control theory. Second, in cognitive tasks involving learning symbolic level action selection, humans learn such problems using model-free and model-based reinforcement learning algorithms. We propose that combining these two levels of abstraction leads to a fast global solution of nonlinear control problems using reduced number of controllers. Our framework learns the local task dynamics from naive experience and forms locally optimal infinite horizon Linear Quadratic Regulators which produce continuous low-level control. A top-level reinforcement learner uses the controllers as actions and learns how to best combine them in state space while maximising a long-term reward. A single optimal control objective function drives high-level symbolic learning by providing training signals on desirability of each selected controller. We show that a small number of locally optimal linear controllers are able to solve global nonlinear control problems with unknown dynamics when combined with a reinforcement learner in this hierarchical framework. Our algorithm competes in terms of computational cost and solution quality with sophisticated control algorithms and we illustrate this with solutions to benchmark problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge