Lossy Neural Compression for Geospatial Analytics: A Review

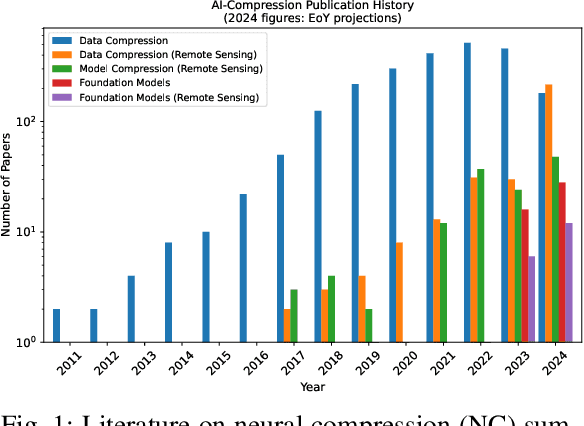
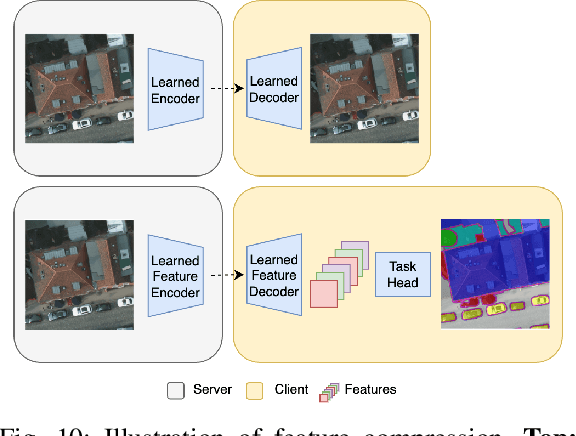
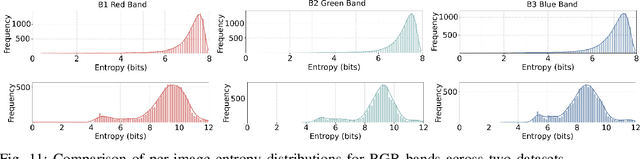
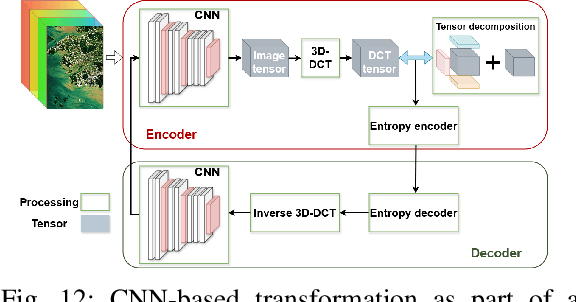
Over the past decades, there has been an explosion in the amount of available Earth Observation (EO) data. The unprecedented coverage of the Earth's surface and atmosphere by satellite imagery has resulted in large volumes of data that must be transmitted to ground stations, stored in data centers, and distributed to end users. Modern Earth System Models (ESMs) face similar challenges, operating at high spatial and temporal resolutions, producing petabytes of data per simulated day. Data compression has gained relevance over the past decade, with neural compression (NC) emerging from deep learning and information theory, making EO data and ESM outputs ideal candidates due to their abundance of unlabeled data. In this review, we outline recent developments in NC applied to geospatial data. We introduce the fundamental concepts of NC including seminal works in its traditional applications to image and video compression domains with focus on lossy compression. We discuss the unique characteristics of EO and ESM data, contrasting them with "natural images", and explain the additional challenges and opportunities they present. Moreover, we review current applications of NC across various EO modalities and explore the limited efforts in ESM compression to date. The advent of self-supervised learning (SSL) and foundation models (FM) has advanced methods to efficiently distill representations from vast unlabeled data. We connect these developments to NC for EO, highlighting the similarities between the two fields and elaborate on the potential of transferring compressed feature representations for machine--to--machine communication. Based on insights drawn from this review, we devise future directions relevant to applications in EO and ESM.

Predicting into unknown space? Estimating the area of applicability of spatial prediction models

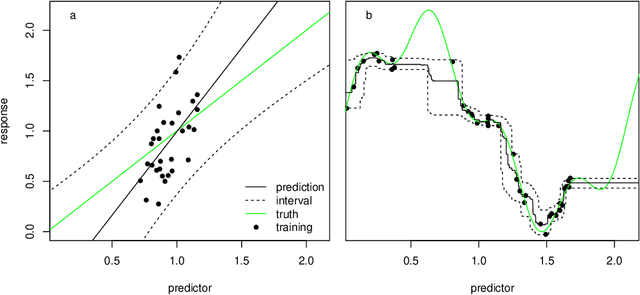
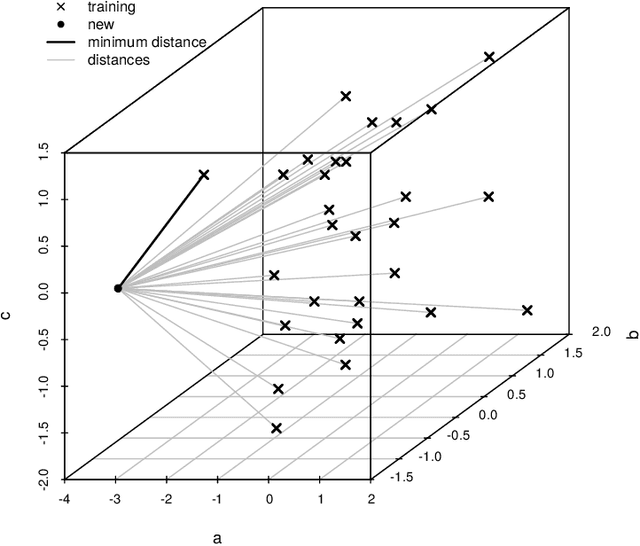
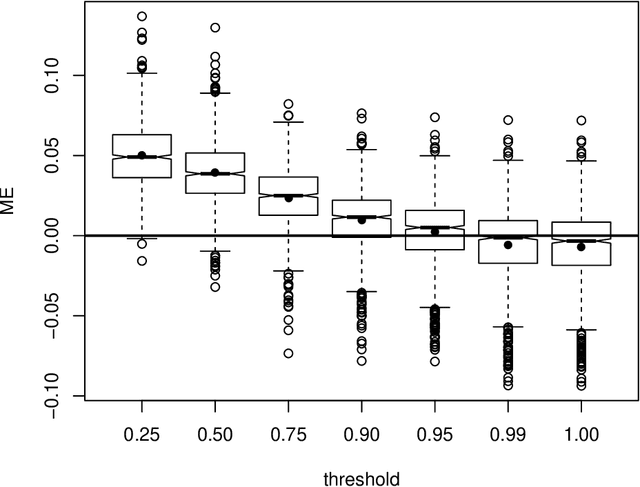
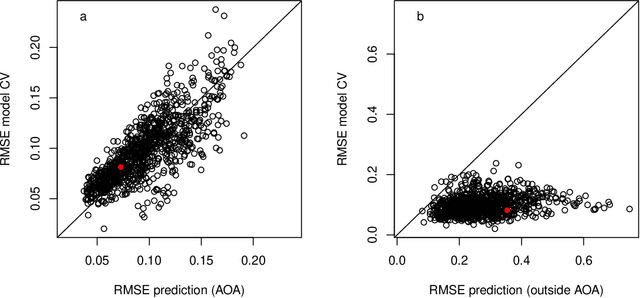
Predictive modelling using machine learning has become very popular for spatial mapping of the environment. Models are often applied to make predictions far beyond sampling locations where new geographic locations might considerably differ from the training data in their environmental properties. However, areas in the predictor space without support of training data are problematic. Since the model has no knowledge about these environments, predictions have to be considered uncertain. Estimating the area to which a prediction model can be reliably applied is required. Here, we suggest a methodology that delineates the "area of applicability" (AOA) that we define as the area, for which the cross-validation error of the model applies. We first propose a "dissimilarity index" (DI) that is based on the minimum distance to the training data in the predictor space, with predictors being weighted by their respective importance in the model. The AOA is then derived by applying a threshold based on the DI of the training data where the DI is calculated with respect to the cross-validation strategy used for model training. We test for the ideal threshold by using simulated data and compare the prediction error within the AOA with the cross-validation error of the model. We illustrate the approach using a simulated case study. Our simulation study suggests a threshold on DI to define the AOA at the .95 quantile of the DI in the training data. Using this threshold, the prediction error within the AOA is comparable to the cross-validation RMSE of the model, while the cross-validation error does not apply outside the AOA. This applies to models being trained with randomly distributed training data, as well as when training data are clustered in space and where spatial cross-validation is applied. We suggest to report the AOA alongside predictions, complementary to validation measures.