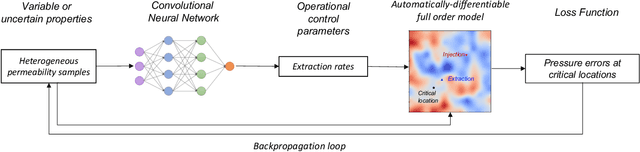
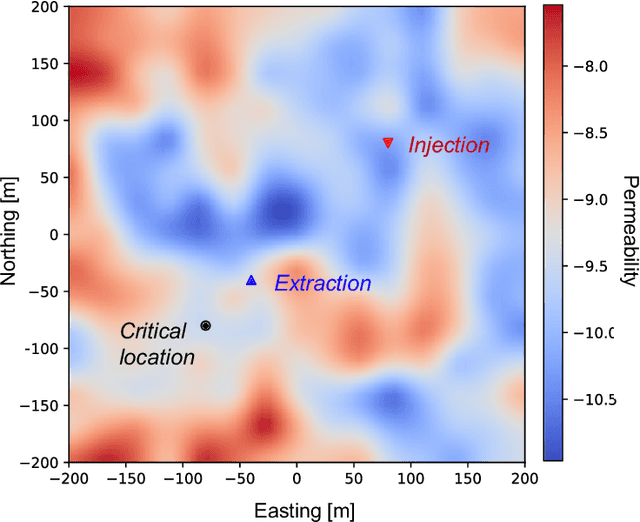
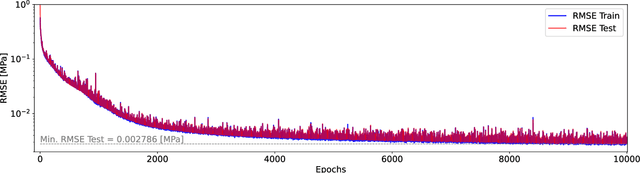
Physics-informed machine learning with differentiable programming for heterogeneous underground reservoir pressure management

Avoiding over-pressurization in subsurface reservoirs is critical for applications like CO2 sequestration and wastewater injection. Managing the pressures by controlling injection/extraction are challenging because of complex heterogeneity in the subsurface. The heterogeneity typically requires high-fidelity physics-based models to make predictions on CO$_2$ fate. Furthermore, characterizing the heterogeneity accurately is fraught with parametric uncertainty. Accounting for both, heterogeneity and uncertainty, makes this a computationally-intensive problem challenging for current reservoir simulators. To tackle this, we use differentiable programming with a full-physics model and machine learning to determine the fluid extraction rates that prevent over-pressurization at critical reservoir locations. We use DPFEHM framework, which has trustworthy physics based on the standard two-point flux finite volume discretization and is also automatically differentiable like machine learning models. Our physics-informed machine learning framework uses convolutional neural networks to learn an appropriate extraction rate based on the permeability field. We also perform a hyperparameter search to improve the model's accuracy. Training and testing scenarios are executed to evaluate the feasibility of using physics-informed machine learning to manage reservoir pressures. We constructed and tested a sufficiently accurate simulator that is 400000 times faster than the underlying physics-based simulator, allowing for near real-time analysis and robust uncertainty quantification.

A Robust Deep Learning Workflow to Predict Multiphase Flow Behavior during Geological CO2 Sequestration Injection and Post-Injection Periods

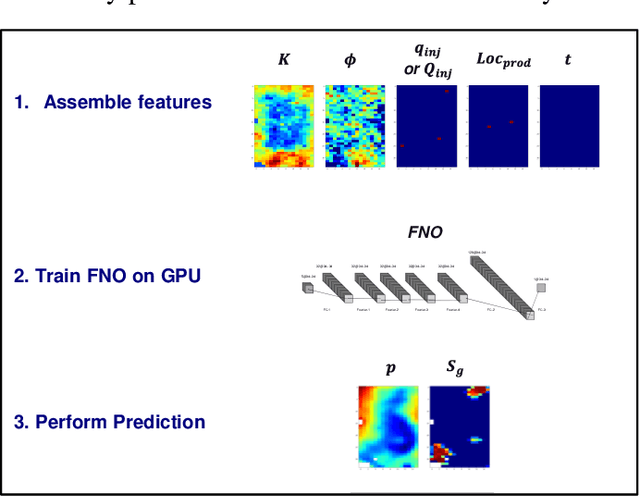
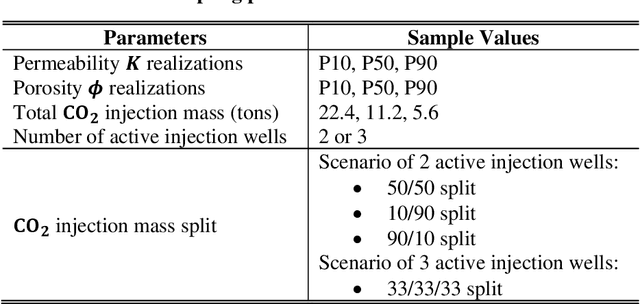
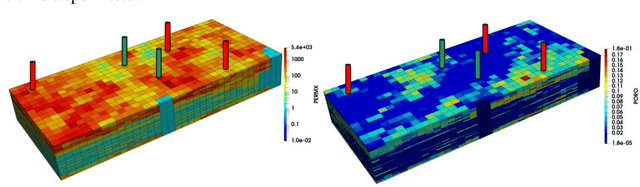
This paper contributes to the development and evaluation of a deep learning workflow that accurately and efficiently predicts the temporal-spatial evolution of pressure and CO2 plumes during injection and post-injection periods of geologic CO2 sequestration (GCS) operations. Based on a Fourier Neuron Operator, the deep learning workflow takes input variables or features including rock properties, well operational controls and time steps, and predicts the state variables of pressure and CO2 saturation. To further improve the predictive fidelity, separate deep learning models are trained for CO2 injection and post-injection periods due the difference in primary driving force of fluid flow and transport during these two phases. We also explore different combinations of features to predict the state variables. We use a realistic example of CO2 injection and storage in a 3D heterogeneous saline aquifer, and apply the deep learning workflow that is trained from physics-based simulation data and emulate the physics process. Through this numerical experiment, we demonstrate that using two separate deep learning models to distinguish post-injection from injection period generates the most accurate prediction of pressure, and a single deep learning model of the whole GCS process including the cumulative injection volume of CO2 as a deep learning feature, leads to the most accurate prediction of CO2 saturation. For the post-injection period, it is key to use cumulative CO2 injection volume to inform the deep learning models about the total carbon storage when predicting either pressure or saturation. The deep learning workflow not only provides high predictive fidelity across temporal and spatial scales, but also offers a speedup of 250 times compared to full physics reservoir simulation, and thus will be a significant predictive tool for engineers to manage the long term process of GCS.

Improving Deep Learning Performance for Predicting Large-Scale Porous-Media Flow through Feature Coarsening

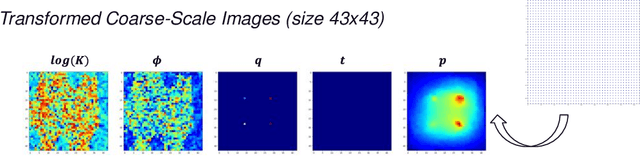
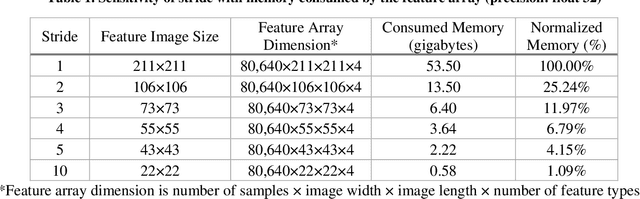
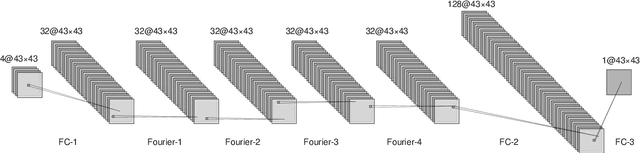
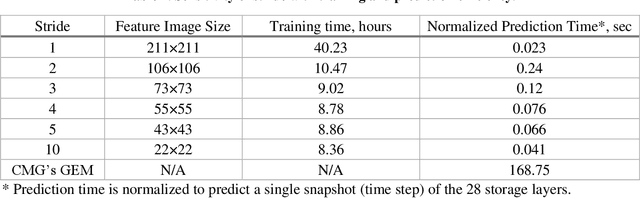
Physics-based simulation for fluid flow in porous media is a computational technology to predict the temporal-spatial evolution of state variables (e.g. pressure) in porous media, and usually requires high computational expense due to its nonlinearity and the scale of the study domain. This letter describes a deep learning (DL) workflow to predict the pressure evolution as fluid flows in large-scale 3D heterogeneous porous media. In particular, we apply feature coarsening technique to extract the most representative information and perform the training and prediction of DL at the coarse scale, and further recover the resolution at the fine scale by 2D piecewise cubic interpolation. We validate the DL approach that is trained from physics-based simulation data to predict pressure field in a field-scale 3D geologic CO_2 storage reservoir. We evaluate the impact of feature coarsening on DL performance, and observe that the feature coarsening can not only decrease training time by >74% and reduce memory consumption by >75%, but also maintains temporal error <1.5%. Besides, the DL workflow provides predictive efficiency with ~1400 times speedup compared to physics-based simulation.

A Physics-Constrained Deep Learning Model for Simulating Multiphase Flow in 3D Heterogeneous Porous Media

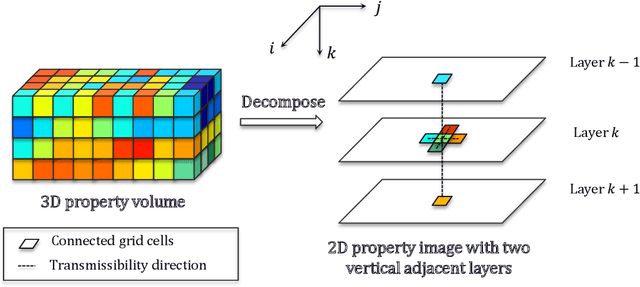
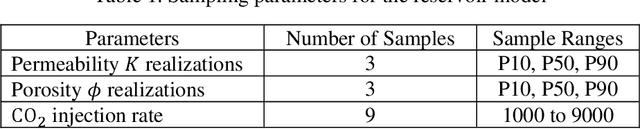
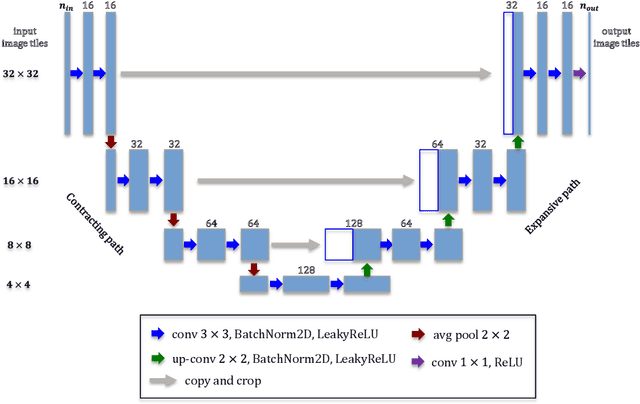
In this work, an efficient physics-constrained deep learning model is developed for solving multiphase flow in 3D heterogeneous porous media. The model fully leverages the spatial topology predictive capability of convolutional neural networks, and is coupled with an efficient continuity-based smoother to predict flow responses that need spatial continuity. Furthermore, the transient regions are penalized to steer the training process such that the model can accurately capture flow in these regions. The model takes inputs including properties of porous media, fluid properties and well controls, and predicts the temporal-spatial evolution of the state variables (pressure and saturation). While maintaining the continuity of fluid flow, the 3D spatial domain is decomposed into 2D images for reducing training cost, and the decomposition results in an increased number of training data samples and better training efficiency. Additionally, a surrogate model is separately constructed as a postprocessor to calculate well flow rate based on the predictions of state variables from the deep learning model. We use the example of CO2 injection into saline aquifers, and apply the physics-constrained deep learning model that is trained from physics-based simulation data and emulates the physics process. The model performs prediction with a speedup of ~1400 times compared to physics-based simulations, and the average temporal errors of predicted pressure and saturation plumes are 0.27% and 0.099% respectively. Furthermore, water production rate is efficiently predicted by a surrogate model for well flow rate, with a mean error less than 5%. Therefore, with its unique scheme to cope with the fidelity in fluid flow in porous media, the physics-constrained deep learning model can become an efficient predictive model for computationally demanding inverse problems or other coupled processes.

A Gradient-based Deep Neural Network Model for Simulating Multiphase Flow in Porous Media

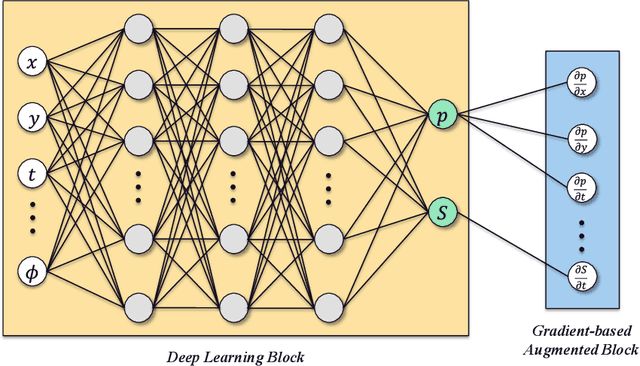
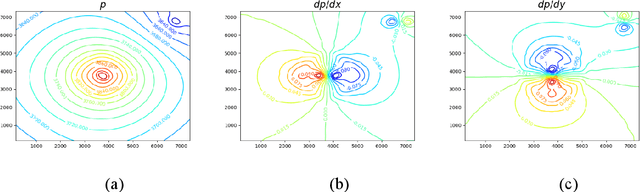
Simulation of multiphase flow in porous media is crucial for the effective management of subsurface energy and environment related activities. The numerical simulators used for modeling such processes rely on spatial and temporal discretization of the governing partial-differential equations (PDEs) into algebraic systems via numerical methods. These simulators usually require dedicated software development and maintenance, and suffer low efficiency from a runtime and memory standpoint. Therefore, developing cost-effective, data-driven models can become a practical choice since deep learning approaches are considered to be universal approximations. In this paper, we describe a gradient-based deep neural network (GDNN) constrained by the physics related to multiphase flow in porous media. We tackle the nonlinearity of flow in porous media induced by rock heterogeneity, fluid properties and fluid-rock interactions by decomposing the nonlinear PDEs into a dictionary of elementary differential operators. We use a combination of operators to handle rock spatial heterogeneity and fluid flow by advection. Since the augmented differential operators are inherently related to the physics of fluid flow, we treat them as first principles prior knowledge to regularize the GDNN training. We use the example of pressure management at geologic CO2 storage sites, where CO2 is injected in saline aquifers and brine is produced, and apply GDNN to construct a predictive model that is trained from physics-based simulation data and emulates the physics process. We demonstrate that GDNN can effectively predict the nonlinear patterns of subsurface responses including the temporal-spatial evolution of the pressure and saturation plumes. GDNN has great potential to tackle challenging problems that are governed by highly nonlinear physics and enables development of data-driven models with higher fidelity.