Rajesh Pawar
A Physics-Constrained Deep Learning Model for Simulating Multiphase Flow in 3D Heterogeneous Porous Media
Apr 30, 2021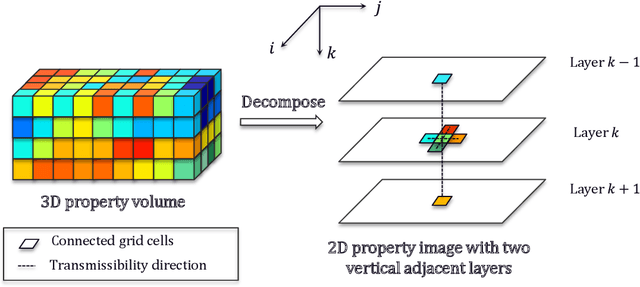
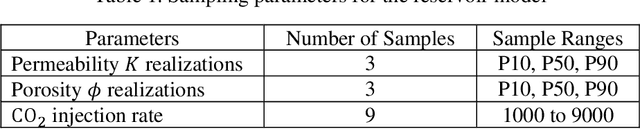
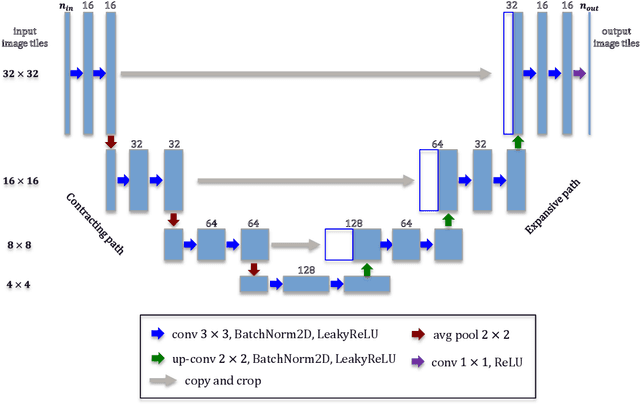

Abstract:In this work, an efficient physics-constrained deep learning model is developed for solving multiphase flow in 3D heterogeneous porous media. The model fully leverages the spatial topology predictive capability of convolutional neural networks, and is coupled with an efficient continuity-based smoother to predict flow responses that need spatial continuity. Furthermore, the transient regions are penalized to steer the training process such that the model can accurately capture flow in these regions. The model takes inputs including properties of porous media, fluid properties and well controls, and predicts the temporal-spatial evolution of the state variables (pressure and saturation). While maintaining the continuity of fluid flow, the 3D spatial domain is decomposed into 2D images for reducing training cost, and the decomposition results in an increased number of training data samples and better training efficiency. Additionally, a surrogate model is separately constructed as a postprocessor to calculate well flow rate based on the predictions of state variables from the deep learning model. We use the example of CO2 injection into saline aquifers, and apply the physics-constrained deep learning model that is trained from physics-based simulation data and emulates the physics process. The model performs prediction with a speedup of ~1400 times compared to physics-based simulations, and the average temporal errors of predicted pressure and saturation plumes are 0.27% and 0.099% respectively. Furthermore, water production rate is efficiently predicted by a surrogate model for well flow rate, with a mean error less than 5%. Therefore, with its unique scheme to cope with the fidelity in fluid flow in porous media, the physics-constrained deep learning model can become an efficient predictive model for computationally demanding inverse problems or other coupled processes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge