A Gradient-based Deep Neural Network Model for Simulating Multiphase Flow in Porous Media
Paper and Code
Apr 30, 2021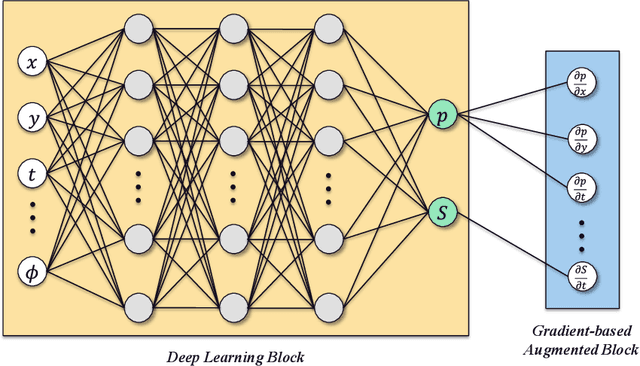

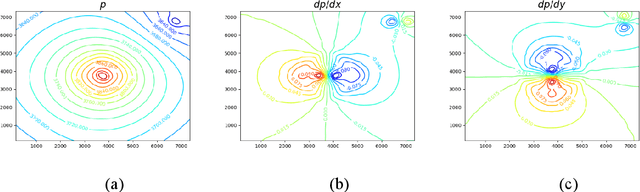
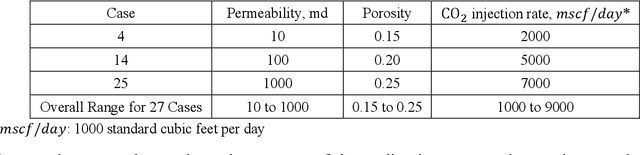
Simulation of multiphase flow in porous media is crucial for the effective management of subsurface energy and environment related activities. The numerical simulators used for modeling such processes rely on spatial and temporal discretization of the governing partial-differential equations (PDEs) into algebraic systems via numerical methods. These simulators usually require dedicated software development and maintenance, and suffer low efficiency from a runtime and memory standpoint. Therefore, developing cost-effective, data-driven models can become a practical choice since deep learning approaches are considered to be universal approximations. In this paper, we describe a gradient-based deep neural network (GDNN) constrained by the physics related to multiphase flow in porous media. We tackle the nonlinearity of flow in porous media induced by rock heterogeneity, fluid properties and fluid-rock interactions by decomposing the nonlinear PDEs into a dictionary of elementary differential operators. We use a combination of operators to handle rock spatial heterogeneity and fluid flow by advection. Since the augmented differential operators are inherently related to the physics of fluid flow, we treat them as first principles prior knowledge to regularize the GDNN training. We use the example of pressure management at geologic CO2 storage sites, where CO2 is injected in saline aquifers and brine is produced, and apply GDNN to construct a predictive model that is trained from physics-based simulation data and emulates the physics process. We demonstrate that GDNN can effectively predict the nonlinear patterns of subsurface responses including the temporal-spatial evolution of the pressure and saturation plumes. GDNN has great potential to tackle challenging problems that are governed by highly nonlinear physics and enables development of data-driven models with higher fidelity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge