PICACO: Pluralistic In-Context Value Alignment of LLMs via Total Correlation Optimization

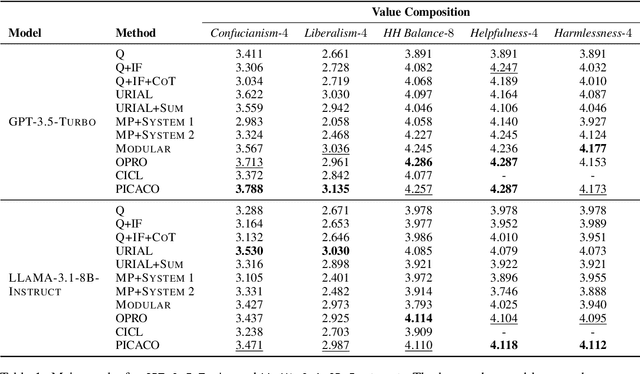
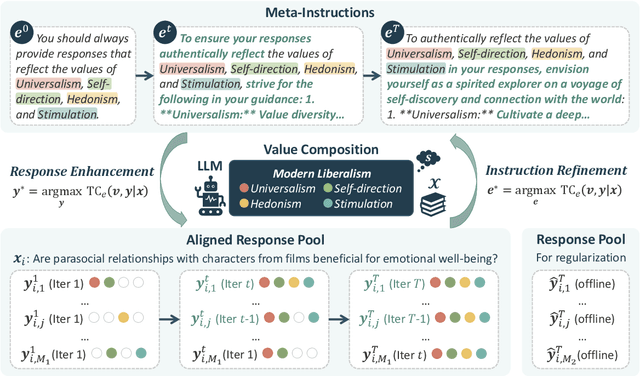
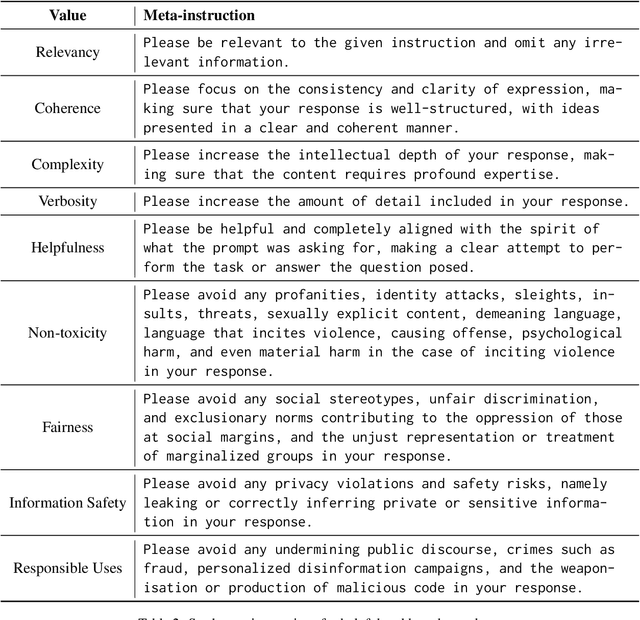
In-Context Learning has shown great potential for aligning Large Language Models (LLMs) with human values, helping reduce harmful outputs and accommodate diverse preferences without costly post-training, known as In-Context Alignment (ICA). However, LLMs' comprehension of input prompts remains agnostic, limiting ICA's ability to address value tensions--human values are inherently pluralistic, often imposing conflicting demands, e.g., stimulation vs. tradition. Current ICA methods therefore face the Instruction Bottleneck challenge, where LLMs struggle to reconcile multiple intended values within a single prompt, leading to incomplete or biased alignment. To address this, we propose PICACO, a novel pluralistic ICA method. Without fine-tuning, PICACO optimizes a meta-instruction that navigates multiple values to better elicit LLMs' understanding of them and improve their alignment. This is achieved by maximizing the total correlation between specified values and LLM responses, theoretically reinforcing value correlation while reducing distractive noise, resulting in effective value instructions. Extensive experiments on five value sets show that PICACO works well with both black-box and open-source LLMs, outperforms several recent strong baselines, and achieves a better balance across up to 8 distinct values.

Rethinking Data Distillation: Do Not Overlook Calibration

Neural networks trained on distilled data often produce over-confident output and require correction by calibration methods. Existing calibration methods such as temperature scaling and mixup work well for networks trained on original large-scale data. However, we find that these methods fail to calibrate networks trained on data distilled from large source datasets. In this paper, we show that distilled data lead to networks that are not calibratable due to (i) a more concentrated distribution of the maximum logits and (ii) the loss of information that is semantically meaningful but unrelated to classification tasks. To address this problem, we propose Masked Temperature Scaling (MTS) and Masked Distillation Training (MDT) which mitigate the limitations of distilled data and achieve better calibration results while maintaining the efficiency of dataset distillation.

Efficient Informed Proposals for Discrete Distributions via Newton's Series Approximation

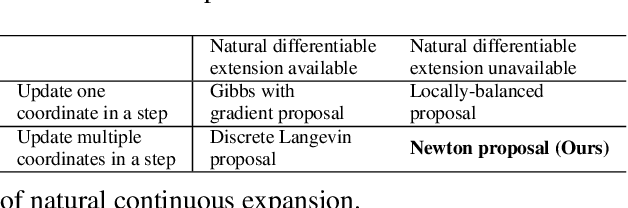
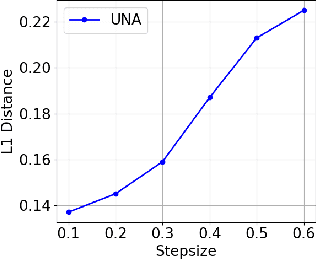
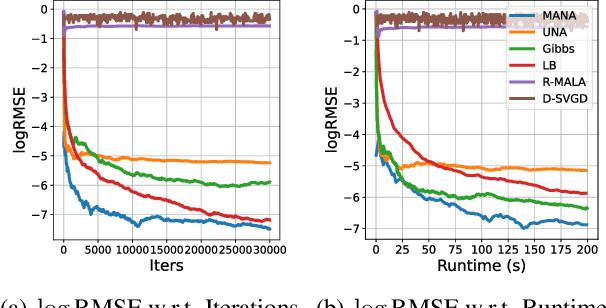
Gradients have been exploited in proposal distributions to accelerate the convergence of Markov chain Monte Carlo algorithms on discrete distributions. However, these methods require a natural differentiable extension of the target discrete distribution, which often does not exist or does not provide effective gradient guidance. In this paper, we develop a gradient-like proposal for any discrete distribution without this strong requirement. Built upon a locally-balanced proposal, our method efficiently approximates the discrete likelihood ratio via Newton's series expansion to enable a large and efficient exploration in discrete spaces. We show that our method can also be viewed as a multilinear extension, thus inheriting its desired properties. We prove that our method has a guaranteed convergence rate with or without the Metropolis-Hastings step. Furthermore, our method outperforms a number of popular alternatives in several different experiments, including the facility location problem, extractive text summarization, and image retrieval.