Joint 9D Receiver Localization and Ephemeris Correction with LEO and $5$G Base Stations

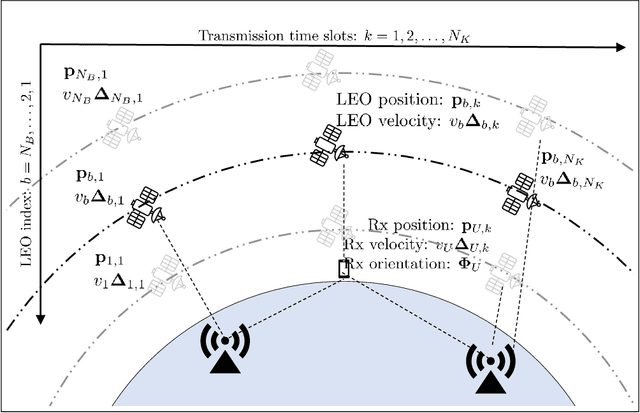
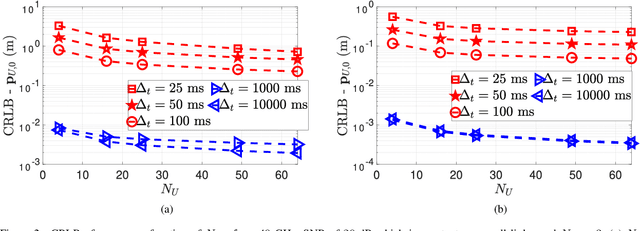
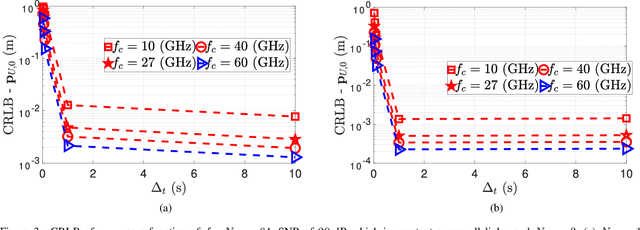
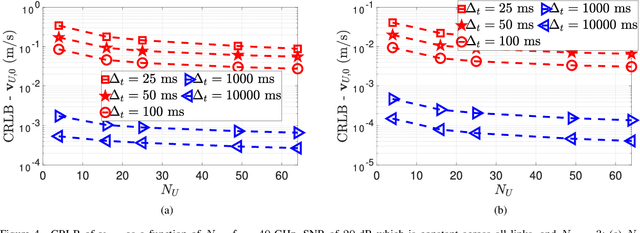
In this paper, we use the Fisher information matrix (FIM) to analyze the interaction between low-earth orbit (LEO) satellites and $5$G base stations in providing $9$D receiver localization and correcting LEO ephemeris. First, we give a channel model that captures all the information in the LEO-receiver, LEO-BS, and BS-receiver links. Subsequently, we use FIM to capture the amount of information about the channel parameters in these links. Then, we transform these FIM for channel parameters to the FIM for the $9$D ($3$D position, $3$D orientation, and $3$D velocity estimation) receiver localization parameters and the LEO position and velocity offset. Closed-form expressions for the entries in the FIM for these location parameters are presented. Our results on identifiability utilizing the FIM for the location parameters indicate: i) with one LEO, we need three BSs and three time slots to both estimate the $9$D location parameters and correct the LEO position and velocity, ii) with two LEO, we need three BSs and three time slots to both estimate the $9$D location parameters and correct the LEO position and velocity, and iii) with three LEO, we need three BSs and four-time slots to both estimate the $9$D location parameters and correct the LEO position and velocity. Another key insight is that through the Cramer Rao lower bound we show that with a single LEO, three time slots, and three BSs, the receiver positioning error, velocity estimation error, orientation error, LEO position offset estimation error, and LEO velocity offset estimation error are $0.1 \text{ cm}$, $1 \text{ mm/s}$, $10^{-3} \text{ rad}$, $0.01 \text{ m}$, and $1 \text{ m/s}$, respectively.

Fundamentals of LEO Based Localization

In this paper, we derive the fundamental limits of low earth orbit (LEO) enabled localization by analyzing the available information in signals from multiple LEOs during different transmission time slots received on a multiple antennas and evaluate the utility of these signals for $9$D localization ($3$D position, $3$D orientation, and $3$D velocity estimation). We start by deriving the Fisher Information Matrix (FIM) for the channel parameters that are present in the signals received from LEOs in the same or multiple constellations during multiple transmission time slots. To accomplish this, we define a system model that captures i) time offset between LEOs caused by having relatively cheap clocks, ii) frequency offset between LEOs, iii) the unknown Doppler rate caused by high mobility LEOs, and iv) multiple transmission time slots from a particular LEO. We transform the FIM for the channel parameters to the FIM for the location parameters and determine the required conditions for localization. To do this, we start with the $3$D localization cases: i) $3$D positioning with known velocity and orientation, ii) $3$D orientation estimation with known position and velocity, and iii) $3$D velocity estimation with known position and orientation. Subsequently, we derive the FIM for the full $9$D localization case ($3$D position, $3$D orientation, and $3$D velocity estimation) in terms of the FIM for the $3$D localization. Using these results, we determine the number of LEOs, the operating frequency, the number of transmission time slots, and the number of receive antennas that allow for different levels of location estimation.

On the Limits of Single Anchor Localization: Near-Field vs Far-Field

It is well known that a single anchor can be used to determine the position and orientation of an agent communicating with it. However, it is not clear what information about the anchor or the agent is necessary to perform this localization, especially when the agent is in the near-field of the anchor. Hence, in this paper, to investigate the limits of localizing an agent with some uncertainty in the anchor location, we consider a wireless link consisting of source and destination nodes. More specifically, we present a Fisher information theoretical investigation of the possibility of estimating different combinations of the source and destination's position and orientation from the signal received at the destination. To present a comprehensive study, we perform this Fisher information theoretic investigation under both the near and far field propagation models. One of the key insights is that while the source or destination's $3$D orientation can be jointly estimated with the source or destination's $3$D position in the near-field propagation regime, only the source or destination's $2$D orientation can be jointly estimated with the source or destination's $2$D position in the far-field propagation regime. Also, a simulation of the FIM indicates that in the near-field, we can estimate the source's $3$D orientation angles with no beamforming, but in the far-field, we can not estimate the source's $2$D orientation angles when no beamforming is employed.

RIS-Aided Kinematic Analysis for Remote Rehabilitation

This paper is the first to introduce the idea of using reconfigurable intelligent surfaces (RISs) as passive devices that measure the position and orientation of certain human body parts over time. In this paper, we investigate the possibility of utilizing the available geometric information provided by on-body RISs that reflect signals from an off-body transmitter to an off-body receiver for stroke rehabilitation. More specifically, we investigate the possibility of using on-body RISs to estimate the location information over time of upper limbs that may have been impaired due to stroke. This location information can help medical professionals to estimate the possibly time varying pose and obtain progress on the rehabilitation of the upper limbs. Our analysis is focused on two scenarios: i) after assessment exercises for stroke rehabilitation when the upper limbs are resting at predefined points in the rehabilitation center, and ii) during the assessment exercises. In the first scenario, we explore the possibility of upper limb orientation estimation by deriving the Fisher information matrix (FIM) under near-field and far-field propagation conditions. It is noteworthy that the FIM quantifies how accurately we can estimate location information from a signal, and any subsequent algorithm is bounded by a function of the FIM. Coming to our propagation assumptions, the difference between the near-field and far-field regimes lies in the curvature of the wavefront. In the near-field, a receiver experiences a spherical wavefront, whereas in the far-field, the wavefront is approximately linear. The threshold to be within the near-field can be on the order of $10 \text{ m}.$

Iterative RNDOP-Optimal Anchor Placement for Beyond Convex Hull ToA-based Localization: Performance Bounds and Heuristic Algorithms

Localizing targets outside the anchors' convex hull is an understudied but prevalent scenario in vehicle-centric, UAV-based, and self-localization applications. Considering such scenarios, this paper studies the optimal anchor placement problem for Time-of-Arrival (ToA)-based localization schemes such that the worst-case Dilution of Precision (DOP) is minimized. Building on prior results on DOP scaling laws for beyond convex hull ToA-based localization, we propose a novel metric termed the Range-Normalized DOP (RNDOP). We show that the worst-case DOP-optimal anchor placement problem simplifies to a min-max RNDOP-optimal anchor placement problem. Unfortunately, this formulation results in a non-convex and intractable problem under realistic constraints. To overcome this, we propose iterative anchor addition schemes, which result in a tractable albeit non-convex problem. By exploiting the structure arising from the resultant rank-1 update, we devise three heuristic schemes with varying performance-complexity tradeoffs. In addition, we also derive the upper and lower bounds for scenarios where we are placing anchors to optimize the worst-case (a) 3D positioning error and (b) 2D positioning error. We build on these results to design a cohesive iterative algorithmic framework for robust anchor placement and then discuss the computational complexity of the proposed schemes. Using numerical results, we validate the accuracy of our theoretical results. We also present comprehensive Monte-Carlo simulation results to compare the positioning error and execution time performance of each iterative scheme, discuss the tradeoffs, and provide valuable system design insights for beyond convex hull localization scenarios.

RIS-Aided Localization under Position and Orientation Offsets in the Near and Far Field

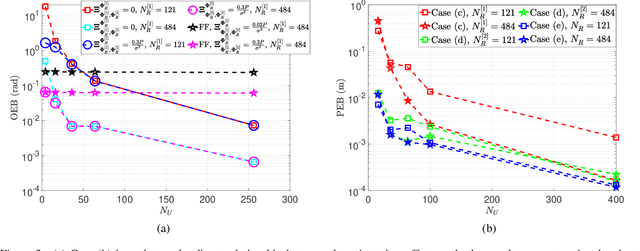
This paper presents a rigorous Bayesian analysis of the information in the signal (consisting of both the line-of-sight (LOS) path and reflections from multiple RISs) that originate from a single base station (BS) and is received by a user equipment (UE). For a comprehensive Bayesian analysis, both near and far field regimes are considered. The Bayesian analysis views both the location of the RISs and previous information about the UE as {\em a priori} information for UE localization. With outdated {\em a priori} information, the position and orientation offsets of the RISs become parameters that need to be estimated and fed back to the BS for correction. We first show that when the RIS elements have a half wavelength spacing, this RIS orientation offset is a factor in the pathloss of the RIS paths. Subsequently, we show through the Bayesian equivalent FIM (EFIM) for the channel parameters that the RIS orientation offset cannot be corrected when there is an unknown phase offset in the received signal in the far-field regime. However, the corresponding EFIM for the channel parameters in the received signal observed in the near-field shows that this unknown phase offset does not hinder the estimation of the RIS orientation offset when the UE has more than one receive antenna. Furthermore, we use the EFIM for the UE location parameters to present bounds for UE localization in the presence of RIS uncertainty. We rigorously show that regardless of size and propagation regime, the RISs are only helpful for localization when there is {\em a priori} information about the location of the RISs. Finally, through numerical analysis of the EFIM and its smallest eigenvalue, we demonstrate the loss in information when the far-field model is {\em incorrectly} applied to the signals received at a UE experiencing near-field propagation.

Fundamentals of RIS-Aided Localization in the Far-Field

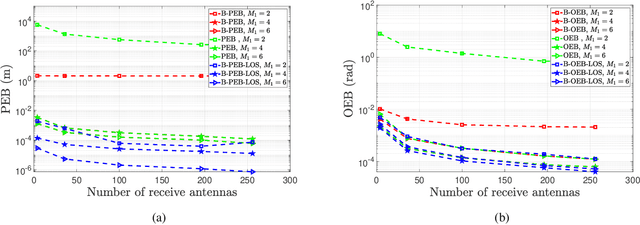
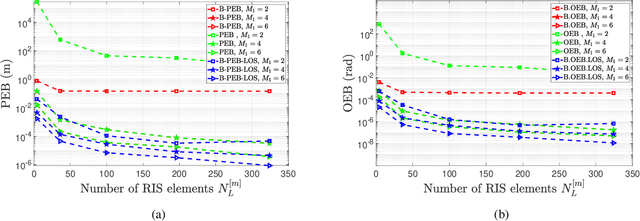
This paper develops fundamental bounds for localization in wireless systems aided by reconfigurable intelligent surfaces (RISs). Specifically, we start from the assumption that the position and orientation of a RIS can be viewed as prior information for RIS-aided localization in wireless systems and derive Bayesian bounds for the localization of a user equipment (UE). To do this, we first derive the Bayesian Fisher information matrix (FIM) for geometric channel parameters in order to derive the Bayesian localization bounds. Subsequently, we show through the equivalent Fisher information matrix (EFIM) that all the information provided by the RIS-related geometric channel parameters is completely lost when the complex path gains are unknown. More specifically, in the absence of channel knowledge, the EFIM of the RIS-related geometric channel parameters is a zero matrix. This observation is crucial to parametric channel estimation. It mandates that any parametric channel estimator must estimate the complex path gains before estimating the RIS-related geometric channel parameters. Furthermore, we note that because these RIS-related geometric parameters are needed for localization, prior information about the complex path gains must be available for feasible UE localization. We also show that this FIM is decomposable into i) information provided by the transmitter, ii) information provided by the RIS, and iii) information provided by the receiver. We then transform the Bayesian EFIM for geometric channel parameters to the Bayesian FIM for the UE position and orientation parameters and examine its specific structure under a particular class of RIS reflection coefficients. Finally, we show the effect of having a set of RISs with perturbed position/orientation on localization performance through numerical results.

Differential Modulation in Massive MIMO With Low-Resolution ADCs

In this paper, we present a differential modulation and detection scheme for use in the uplink of a system with a large number of antennas at the base station, each equipped with low-resolution analog-to-digital converters (ADCs). We derive an expression for the maximum likelihood (ML) detector of a differentially encoded phase information symbol received by a base station operating in the low-resolution ADC regime. We also present an equal performing reduced complexity receiver for detecting the phase information. To increase the supported data rate, we also present a maximum likelihood expression to detect differential amplitude phase shift keying symbols with low-resolution ADCs. We note that the derived detectors are unable to detect the amplitude information. To overcome this limitation, we use the Bussgang Theorem and the Central Limit Theorem (CLT) to develop two detectors capable of detecting the amplitude information. We numerically show that while the first amplitude detector requires multiple quantization bits for acceptable performance, similar performance can be achieved using one-bit ADCs by grouping the receive antennas and employing variable quantization levels (VQL) across distinct antenna groups. We validate the performance of the proposed detectors through simulations and show a comparison with corresponding coherent detectors. Finally, we present a complexity analysis of the proposed low-resolution differential detectors

Differential Deep Detection in Massive MIMO With One-Bit ADC

This article presents a differential detection scheme for the uplink of a massive MIMO system that employs one-bit quantizers on each receive antenna. We focus on the detection of differential amplitude and phase shift keying symbols and we use the Bussgang theorem to express the quantized received signal in terms of quantized signals received during previous channel uses. Subsequently, we derive the maximum likelihood detector for the differentially encoded amplitude and phase information symbols. We note that while the one-bit detector can decode the differentially encoded phase information symbols, it fails to decode the differentially encoded amplitude information. To decode the amplitude information, we present a one-bit variable quantization level (VQL) system and train a deep neural network to perform two-symbol differential amplitude detection. Through Monte-Carlo simulations, we empirically validate the performance of the proposed amplitude and phase detectors. The presented numerical results show that the spectral efficiency attained in one-bit differential systems is better than the spectral efficiency attained in one-bit coherent systems