Fundamentals of RIS-Aided Localization in the Far-Field

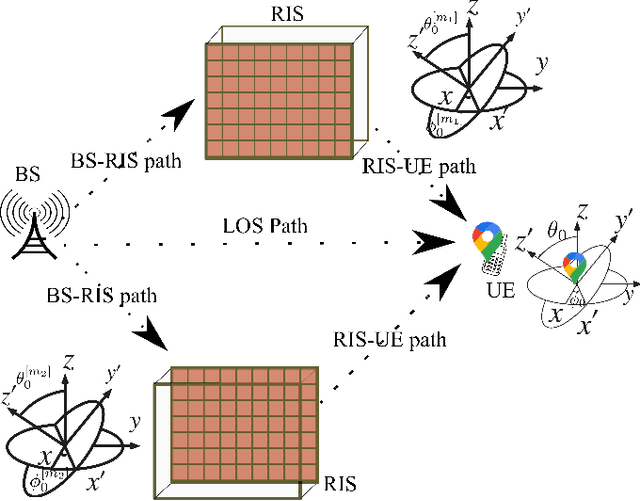
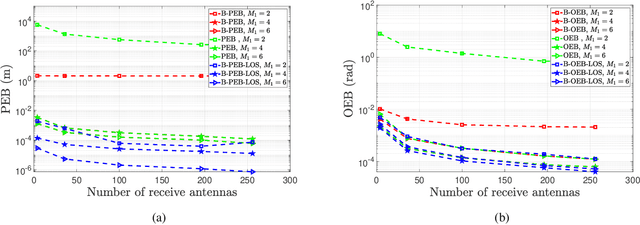
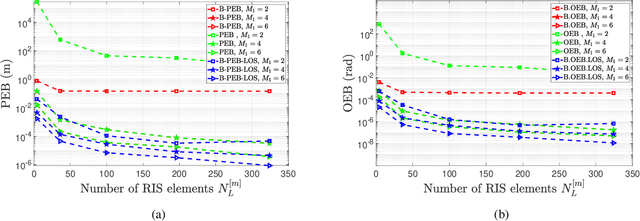
This paper develops fundamental bounds for localization in wireless systems aided by reconfigurable intelligent surfaces (RISs). Specifically, we start from the assumption that the position and orientation of a RIS can be viewed as prior information for RIS-aided localization in wireless systems and derive Bayesian bounds for the localization of a user equipment (UE). To do this, we first derive the Bayesian Fisher information matrix (FIM) for geometric channel parameters in order to derive the Bayesian localization bounds. Subsequently, we show through the equivalent Fisher information matrix (EFIM) that all the information provided by the RIS-related geometric channel parameters is completely lost when the complex path gains are unknown. More specifically, in the absence of channel knowledge, the EFIM of the RIS-related geometric channel parameters is a zero matrix. This observation is crucial to parametric channel estimation. It mandates that any parametric channel estimator must estimate the complex path gains before estimating the RIS-related geometric channel parameters. Furthermore, we note that because these RIS-related geometric parameters are needed for localization, prior information about the complex path gains must be available for feasible UE localization. We also show that this FIM is decomposable into i) information provided by the transmitter, ii) information provided by the RIS, and iii) information provided by the receiver. We then transform the Bayesian EFIM for geometric channel parameters to the Bayesian FIM for the UE position and orientation parameters and examine its specific structure under a particular class of RIS reflection coefficients. Finally, we show the effect of having a set of RISs with perturbed position/orientation on localization performance through numerical results.