BoFire: Bayesian Optimization Framework Intended for Real Experiments

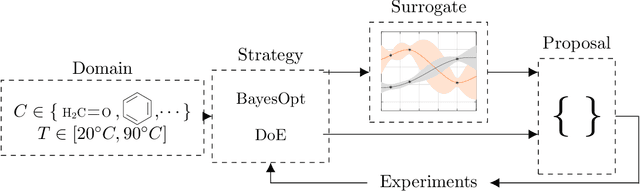
Our open-source Python package BoFire combines Bayesian Optimization (BO) with other design of experiments (DoE) strategies focusing on developing and optimizing new chemistry. Previous BO implementations, for example as they exist in the literature or software, require substantial adaptation for effective real-world deployment in chemical industry. BoFire provides a rich feature-set with extensive configurability and realizes our vision of fast-tracking research contributions into industrial use via maintainable open-source software. Owing to quality-of-life features like JSON-serializability of problem formulations, BoFire enables seamless integration of BO into RESTful APIs, a common architecture component for both self-driving laboratories and human-in-the-loop setups. This paper discusses the differences between BoFire and other BO implementations and outlines ways that BO research needs to be adapted for real-world use in a chemistry setting.

Active Learning of Continuous-time Bayesian Networks through Interventions

We consider the problem of learning structures and parameters of Continuous-time Bayesian Networks (CTBNs) from time-course data under minimal experimental resources. In practice, the cost of generating experimental data poses a bottleneck, especially in the natural and social sciences. A popular approach to overcome this is Bayesian optimal experimental design (BOED). However, BOED becomes infeasible in high-dimensional settings, as it involves integration over all possible experimental outcomes. We propose a novel criterion for experimental design based on a variational approximation of the expected information gain. We show that for CTBNs, a semi-analytical expression for this criterion can be calculated for structure and parameter learning. By doing so, we can replace sampling over experimental outcomes by solving the CTBNs master-equation, for which scalable approximations exist. This alleviates the computational burden of sampling possible experimental outcomes in high-dimensions. We employ this framework in order to recommend interventional sequences. In this context, we extend the CTBN model to conditional CTBNs in order to incorporate interventions. We demonstrate the performance of our criterion on synthetic and real-world data.

Continuous-Time Bayesian Networks with Clocks

Structured stochastic processes evolving in continuous time present a widely adopted framework to model phenomena occurring in nature and engineering. However, such models are often chosen to satisfy the Markov property to maintain tractability. One of the more popular of such memoryless models are Continuous Time Bayesian Networks (CTBNs). In this work, we lift its restriction to exponential survival times to arbitrary distributions. Current extensions achieve this via auxiliary states, which hinder tractability. To avoid that, we introduce a set of node-wise clocks to construct a collection of graph-coupled semi-Markov chains. We provide algorithms for parameter and structure inference, which make use of local dependencies and conduct experiments on synthetic data and a data-set generated through a benchmark tool for gene regulatory networks. In doing so, we point out advantages compared to current CTBN extensions.

A Variational Perturbative Approach to Planning in Graph-based Markov Decision Processes

Coordinating multiple interacting agents to achieve a common goal is a difficult task with huge applicability. This problem remains hard to solve, even when limiting interactions to be mediated via a static interaction-graph. We present a novel approximate solution method for multi-agent Markov decision problems on graphs, based on variational perturbation theory. We adopt the strategy of planning via inference, which has been explored in various prior works. We employ a non-trivial extension of a novel high-order variational method that allows for approximate inference in large networks and has been shown to surpass the accuracy of existing variational methods. To compare our method to two state-of-the-art methods for multi-agent planning on graphs, we apply the method different standard GMDP problems. We show that in cases, where the goal is encoded as a non-local cost function, our method performs well, while state-of-the-art methods approach the performance of random guess. In a final experiment, we demonstrate that our method brings significant improvement for synchronization tasks.

Scalable Structure Learning of Continuous-Time Bayesian Networks from Incomplete Data

Continuous-time Bayesian Networks (CTBNs) represent a compact yet powerful framework for understanding multivariate time-series data. Given complete data, parameters and structure can be estimated efficiently in closed-form. However, if data is incomplete, the latent states of the CTBN have to be estimated by laboriously simulating the intractable dynamics of the assumed CTBN. This is a problem, especially for structure learning tasks, where this has to be done for each element of super-exponentially growing set of possible structures. In order to circumvent this notorious bottleneck, we develop a novel gradient-based approach to structure learning. Instead of sampling and scoring all possible structures individually, we assume the generator of the CTBN to be composed as a mixture of generators stemming from different structures. In this framework, structure learning can be performed via a gradient-based optimization of mixture weights. We combine this approach with a novel variational method that allows for the calculation of the marginal likelihood of a mixture in closed-form. We proof the scalability of our method by learning structures of previously inaccessible sizes from synthetic and real-world data.

Cluster Variational Approximations for Structure Learning of Continuous-Time Bayesian Networks from Incomplete Data

Continuous-time Bayesian networks (CTBNs) constitute a general and powerful framework for modeling continuous-time stochastic processes on networks. This makes them particularly attractive for learning the directed structures among interacting entities. However, if the available data is incomplete, one needs to simulate the prohibitively complex CTBN dynamics. Existing approximation techniques, such as sampling and low-order variational methods, either scale unfavorably in system size, or are unsatisfactory in terms of accuracy. Inspired by recent advances in statistical physics, we present a new approximation scheme based on cluster-variational methods significantly improving upon existing variational approximations. We can analytically marginalize the parameters of the approximate CTBN, as these are of secondary importance for structure learning. This recovers a scalable scheme for direct structure learning from incomplete and noisy time-series data. Our approach outperforms existing methods in terms of scalability.