Forward-Backward Latent State Inference for Hidden Continuous-Time semi-Markov Chains

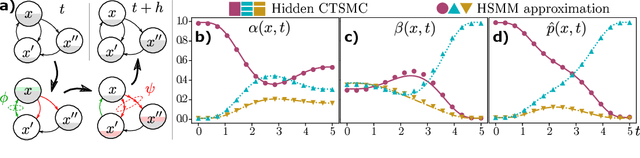
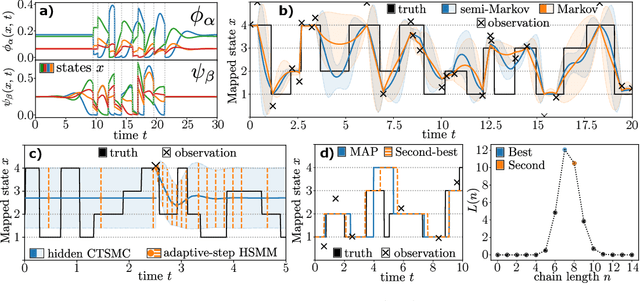
Hidden semi-Markov Models (HSMM's) - while broadly in use - are restricted to a discrete and uniform time grid. They are thus not well suited to explain often irregularly spaced discrete event data from continuous-time phenomena. We show that non-sampling-based latent state inference used in HSMM's can be generalized to latent Continuous-Time semi-Markov Chains (CTSMC's). We formulate integro-differential forward and backward equations adjusted to the observation likelihood and introduce an exact integral equation for the Bayesian posterior marginals and a scalable Viterbi-type algorithm for posterior path estimates. The presented equations can be efficiently solved using well-known numerical methods. As a practical tool, variable-step HSMM's are introduced. We evaluate our approaches in latent state inference scenarios in comparison to classical HSMM's.

Continuous-Time Bayesian Networks with Clocks

Structured stochastic processes evolving in continuous time present a widely adopted framework to model phenomena occurring in nature and engineering. However, such models are often chosen to satisfy the Markov property to maintain tractability. One of the more popular of such memoryless models are Continuous Time Bayesian Networks (CTBNs). In this work, we lift its restriction to exponential survival times to arbitrary distributions. Current extensions achieve this via auxiliary states, which hinder tractability. To avoid that, we introduce a set of node-wise clocks to construct a collection of graph-coupled semi-Markov chains. We provide algorithms for parameter and structure inference, which make use of local dependencies and conduct experiments on synthetic data and a data-set generated through a benchmark tool for gene regulatory networks. In doing so, we point out advantages compared to current CTBN extensions.