Forward-Backward Latent State Inference for Hidden Continuous-Time semi-Markov Chains
Paper and Code
Oct 17, 2022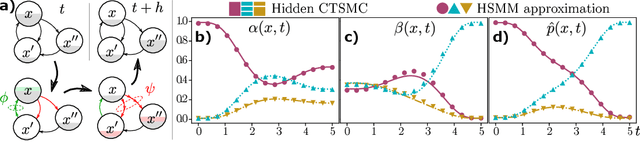
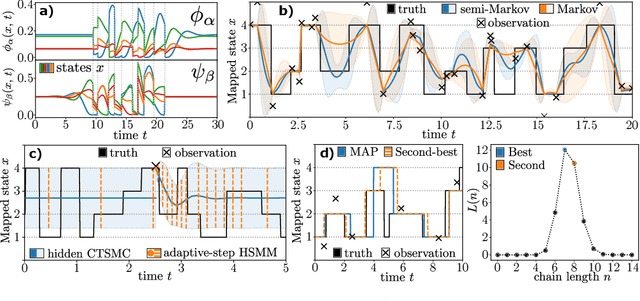
Hidden semi-Markov Models (HSMM's) - while broadly in use - are restricted to a discrete and uniform time grid. They are thus not well suited to explain often irregularly spaced discrete event data from continuous-time phenomena. We show that non-sampling-based latent state inference used in HSMM's can be generalized to latent Continuous-Time semi-Markov Chains (CTSMC's). We formulate integro-differential forward and backward equations adjusted to the observation likelihood and introduce an exact integral equation for the Bayesian posterior marginals and a scalable Viterbi-type algorithm for posterior path estimates. The presented equations can be efficiently solved using well-known numerical methods. As a practical tool, variable-step HSMM's are introduced. We evaluate our approaches in latent state inference scenarios in comparison to classical HSMM's.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge