Generating collective counterfactual explanations in score-based classification via mathematical optimization

Due to the increasing use of Machine Learning models in high stakes decision making settings, it has become increasingly important to have tools to understand how models arrive at decisions. Assuming a trained Supervised Classification model, explanations can be obtained via counterfactual analysis: a counterfactual explanation of an instance indicates how this instance should be minimally modified so that the perturbed instance is classified in the desired class by the Machine Learning classification model. Most of the Counterfactual Analysis literature focuses on the single-instance single-counterfactual setting, in which the analysis is done for one single instance to provide one single explanation. Taking a stakeholder's perspective, in this paper we introduce the so-called collective counterfactual explanations. By means of novel Mathematical Optimization models, we provide a counterfactual explanation for each instance in a group of interest, so that the total cost of the perturbations is minimized under some linking constraints. Making the process of constructing counterfactuals collective instead of individual enables us to detect the features that are critical to the entire dataset to have the individuals classified in the desired class. Our methodology allows for some instances to be treated individually, performing the collective counterfactual analysis for a fraction of records of the group of interest. This way, outliers are identified and handled appropriately. Under some assumptions on the classifier and the space in which counterfactuals are sought, finding collective counterfactuals is reduced to solving a convex quadratic linearly constrained mixed integer optimization problem, which, for datasets of moderate size, can be solved to optimality using existing solvers. The performance of our approach is illustrated on real-world datasets, demonstrating its usefulness.

Supervised Feature Compression based on Counterfactual Analysis

Counterfactual Explanations are becoming a de-facto standard in post-hoc interpretable machine learning. For a given classifier and an instance classified in an undesired class, its counterfactual explanation corresponds to small perturbations of that instance that allows changing the classification outcome. This work aims to leverage Counterfactual Explanations to detect the important decision boundaries of a pre-trained black-box model. This information is used to build a supervised discretization of the features in the dataset with a tunable granularity. Using the discretized dataset, a smaller, therefore more interpretable Decision Tree can be trained, which, in addition, enhances the stability and robustness of the baseline Decision Tree. Numerical results on real-world datasets show the effectiveness of the approach in terms of accuracy and sparsity compared to the baseline Decision Tree.

On Clustering Categories of Categorical Predictors in Generalized Linear Models

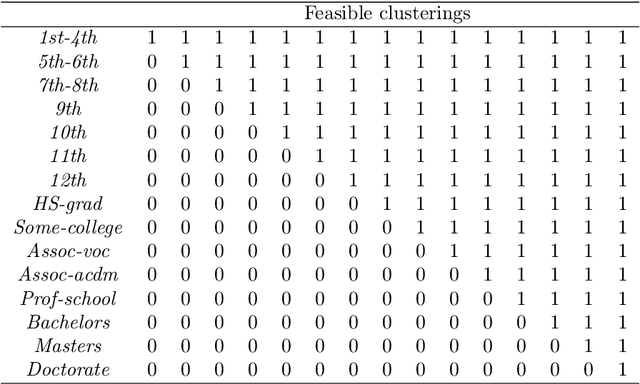
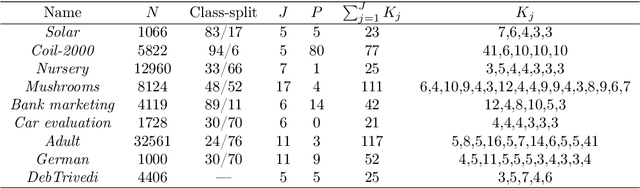
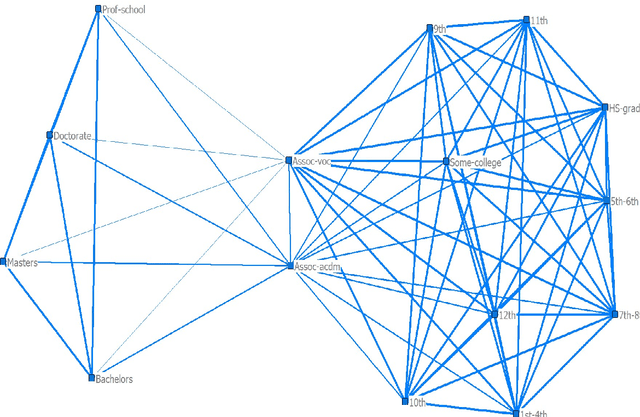
We propose a method to reduce the complexity of Generalized Linear Models in the presence of categorical predictors. The traditional one-hot encoding, where each category is represented by a dummy variable, can be wasteful, difficult to interpret, and prone to overfitting, especially when dealing with high-cardinality categorical predictors. This paper addresses these challenges by finding a reduced representation of the categorical predictors by clustering their categories. This is done through a numerical method which aims to preserve (or even, improve) accuracy, while reducing the number of coefficients to be estimated for the categorical predictors. Thanks to its design, we are able to derive a proximity measure between categories of a categorical predictor that can be easily visualized. We illustrate the performance of our approach in real-world classification and count-data datasets where we see that clustering the categorical predictors reduces complexity substantially without harming accuracy.

Optimal randomized classification trees

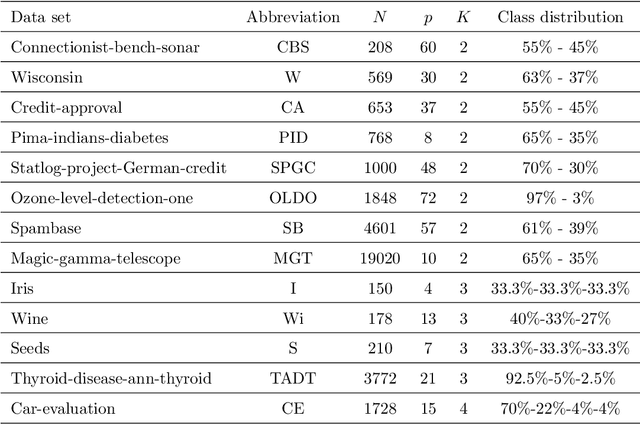
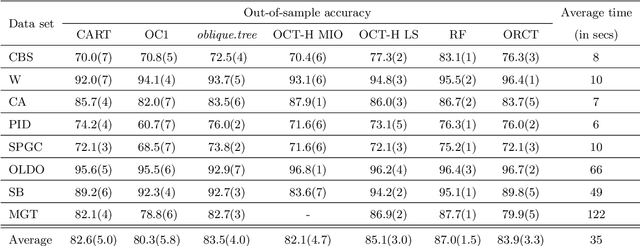
Classification and Regression Trees (CARTs) are off-the-shelf techniques in modern Statistics and Machine Learning. CARTs are traditionally built by means of a greedy procedure, sequentially deciding the splitting predictor variable(s) and the associated threshold. This greedy approach trains trees very fast, but, by its nature, their classification accuracy may not be competitive against other state-of-the-art procedures. Moreover, controlling critical issues, such as the misclassification rates in each of the classes, is difficult. To address these shortcomings, optimal decision trees have been recently proposed in the literature, which use discrete decision variables to model the path each observation will follow in the tree. Instead, we propose a new approach based on continuous optimization. Our classifier can be seen as a randomized tree, since at each node of the decision tree a random decision is made. The computational experience reported demonstrates the good performance of our procedure.

Sparsity in Optimal Randomized Classification Trees

Decision trees are popular Classification and Regression tools and, when small-sized, easy to interpret. Traditionally, a greedy approach has been used to build the trees, yielding a very fast training process; however, controlling sparsity (a proxy for interpretability) is challenging. In recent studies, optimal decision trees, where all decisions are optimized simultaneously, have shown a better learning performance, especially when oblique cuts are implemented. In this paper, we propose a continuous optimization approach to build sparse optimal classification trees, based on oblique cuts, with the aim of using fewer predictor variables in the cuts as well as along the whole tree. Both types of sparsity, namely local and global, are modeled by means of regularizations with polyhedral norms. The computational experience reported supports the usefulness of our methodology. In all our data sets, local and global sparsity can be improved without harming classification accuracy. Unlike greedy approaches, our ability to easily trade in some of our classification accuracy for a gain in global sparsity is shown.