Optimal randomized classification trees

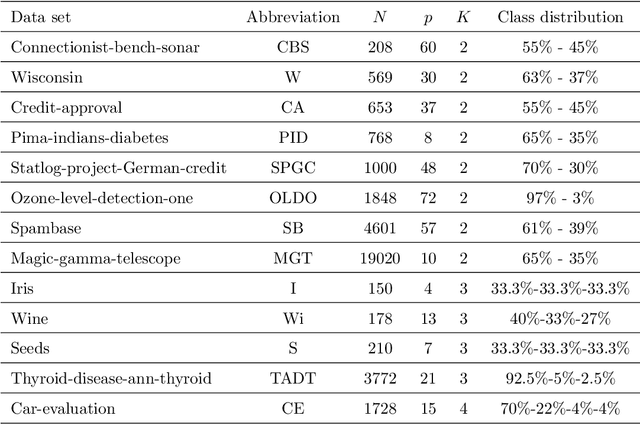
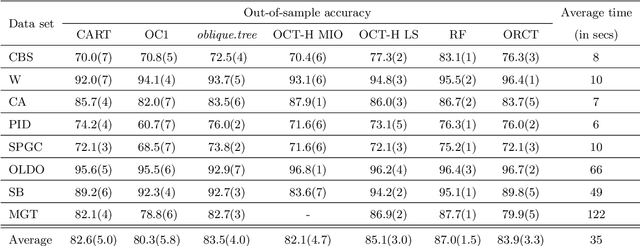
Classification and Regression Trees (CARTs) are off-the-shelf techniques in modern Statistics and Machine Learning. CARTs are traditionally built by means of a greedy procedure, sequentially deciding the splitting predictor variable(s) and the associated threshold. This greedy approach trains trees very fast, but, by its nature, their classification accuracy may not be competitive against other state-of-the-art procedures. Moreover, controlling critical issues, such as the misclassification rates in each of the classes, is difficult. To address these shortcomings, optimal decision trees have been recently proposed in the literature, which use discrete decision variables to model the path each observation will follow in the tree. Instead, we propose a new approach based on continuous optimization. Our classifier can be seen as a randomized tree, since at each node of the decision tree a random decision is made. The computational experience reported demonstrates the good performance of our procedure.

Sparsity in Optimal Randomized Classification Trees

Decision trees are popular Classification and Regression tools and, when small-sized, easy to interpret. Traditionally, a greedy approach has been used to build the trees, yielding a very fast training process; however, controlling sparsity (a proxy for interpretability) is challenging. In recent studies, optimal decision trees, where all decisions are optimized simultaneously, have shown a better learning performance, especially when oblique cuts are implemented. In this paper, we propose a continuous optimization approach to build sparse optimal classification trees, based on oblique cuts, with the aim of using fewer predictor variables in the cuts as well as along the whole tree. Both types of sparsity, namely local and global, are modeled by means of regularizations with polyhedral norms. The computational experience reported supports the usefulness of our methodology. In all our data sets, local and global sparsity can be improved without harming classification accuracy. Unlike greedy approaches, our ability to easily trade in some of our classification accuracy for a gain in global sparsity is shown.