Optimal randomized classification trees
Paper and Code
Oct 19, 2021
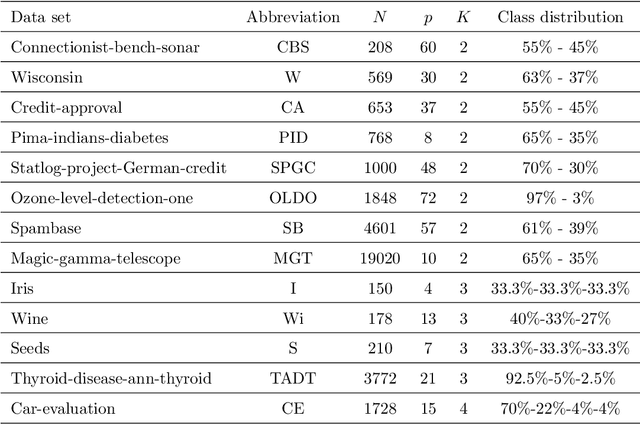

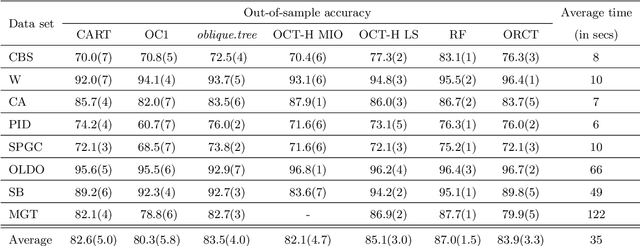
Classification and Regression Trees (CARTs) are off-the-shelf techniques in modern Statistics and Machine Learning. CARTs are traditionally built by means of a greedy procedure, sequentially deciding the splitting predictor variable(s) and the associated threshold. This greedy approach trains trees very fast, but, by its nature, their classification accuracy may not be competitive against other state-of-the-art procedures. Moreover, controlling critical issues, such as the misclassification rates in each of the classes, is difficult. To address these shortcomings, optimal decision trees have been recently proposed in the literature, which use discrete decision variables to model the path each observation will follow in the tree. Instead, we propose a new approach based on continuous optimization. Our classifier can be seen as a randomized tree, since at each node of the decision tree a random decision is made. The computational experience reported demonstrates the good performance of our procedure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge