Variable selection for Naïve Bayes classification

The Na\"ive Bayes has proven to be a tractable and efficient method for classification in multivariate analysis. However, features are usually correlated, a fact that violates the Na\"ive Bayes' assumption of conditional independence, and may deteriorate the method's performance. Moreover, datasets are often characterized by a large number of features, which may complicate the interpretation of the results as well as slow down the method's execution. In this paper we propose a sparse version of the Na\"ive Bayes classifier that is characterized by three properties. First, the sparsity is achieved taking into account the correlation structure of the covariates. Second, different performance measures can be used to guide the selection of features. Third, performance constraints on groups of higher interest can be included. Our proposal leads to a smart search, which yields competitive running times, whereas the flexibility in terms of performance measure for classification is integrated. Our findings show that, when compared against well-referenced feature selection approaches, the proposed sparse Na\"ive Bayes obtains competitive results regarding accuracy, sparsity and running times for balanced datasets. In the case of datasets with unbalanced (or with different importance) classes, a better compromise between classification rates for the different classes is achieved.

A cost-sensitive constrained Lasso

The Lasso has become a benchmark data analysis procedure, and numerous variants have been proposed in the literature. Although the Lasso formulations are stated so that overall prediction error is optimized, no full control over the accuracy prediction on certain individuals of interest is allowed. In this work we propose a novel version of the Lasso in which quadratic performance constraints are added to Lasso-based objective functions, in such a way that threshold values are set to bound the prediction errors in the different groups of interest (not necessarily disjoint). As a result, a constrained sparse regression model is defined by a nonlinear optimization problem. This cost-sensitive constrained Lasso has a direct application in heterogeneous samples where data are collected from distinct sources, as it is standard in many biomedical contexts. Both theoretical properties and empirical studies concerning the new method are explored in this paper. In addition, two illustrations of the method on biomedical and sociological contexts are considered.

Cost-sensitive Feature Selection for Support Vector Machines

Feature Selection is a crucial procedure in Data Science tasks such as Classification, since it identifies the relevant variables, making thus the classification procedures more interpretable, cheaper in terms of measurement and more effective by reducing noise and data overfit. The relevance of features in a classification procedure is linked to the fact that misclassifications costs are frequently asymmetric, since false positive and false negative cases may have very different consequences. However, off-the-shelf Feature Selection procedures seldom take into account such cost-sensitivity of errors. In this paper we propose a mathematical-optimization-based Feature Selection procedure embedded in one of the most popular classification procedures, namely, Support Vector Machines, accommodating asymmetric misclassification costs. The key idea is to replace the traditional margin maximization by minimizing the number of features selected, but imposing upper bounds on the false positive and negative rates. The problem is written as an integer linear problem plus a quadratic convex problem for Support Vector Machines with both linear and radial kernels. The reported numerical experience demonstrates the usefulness of the proposed Feature Selection procedure. Indeed, our results on benchmark data sets show that a substantial decrease of the number of features is obtained, whilst the desired trade-off between false positive and false negative rates is achieved.

On support vector machines under a multiple-cost scenario

Support Vector Machine (SVM) is a powerful tool in binary classification, known to attain excellent misclassification rates. On the other hand, many realworld classification problems, such as those found in medical diagnosis, churn or fraud prediction, involve misclassification costs which may be different in the different classes. However, it may be hard for the user to provide precise values for such misclassification costs, whereas it may be much easier to identify acceptable misclassification rates values. In this paper we propose a novel SVM model in which misclassification costs are considered by incorporating performance constraints in the problem formulation. Specifically, our aim is to seek the hyperplane with maximal margin yielding misclassification rates below given threshold values. Such maximal margin hyperplane is obtained by solving a quadratic convex problem with linear constraints and integer variables. The reported numerical experience shows that our model gives the user control on the misclassification rates in one class (possibly at the expense of an increase in misclassification rates for the other class) and is feasible in terms of running times.

Cost-sensitive probabilistic predictions for support vector machines

Support vector machines (SVMs) are widely used and constitute one of the best examined and used machine learning models for two-class classification. Classification in SVM is based on a score procedure, yielding a deterministic classification rule, which can be transformed into a probabilistic rule (as implemented in off-the-shelf SVM libraries), but is not probabilistic in nature. On the other hand, the tuning of the regularization parameters in SVM is known to imply a high computational effort and generates pieces of information that are not fully exploited, not being used to build a probabilistic classification rule. In this paper we propose a novel approach to generate probabilistic outputs for the SVM. The new method has the following three properties. First, it is designed to be cost-sensitive, and thus the different importance of sensitivity (or true positive rate, TPR) and specificity (true negative rate, TNR) is readily accommodated in the model. As a result, the model can deal with imbalanced datasets which are common in operational business problems as churn prediction or credit scoring. Second, the SVM is embedded in an ensemble method to improve its performance, making use of the valuable information generated in the parameters tuning process. Finally, the probabilities estimation is done via bootstrap estimates, avoiding the use of parametric models as competing approaches. Numerical tests on a wide range of datasets show the advantages of our approach over benchmark procedures.

Optimal randomized classification trees

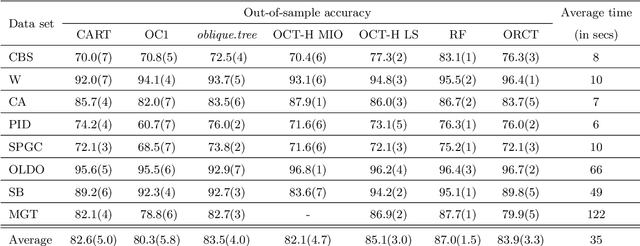
Classification and Regression Trees (CARTs) are off-the-shelf techniques in modern Statistics and Machine Learning. CARTs are traditionally built by means of a greedy procedure, sequentially deciding the splitting predictor variable(s) and the associated threshold. This greedy approach trains trees very fast, but, by its nature, their classification accuracy may not be competitive against other state-of-the-art procedures. Moreover, controlling critical issues, such as the misclassification rates in each of the classes, is difficult. To address these shortcomings, optimal decision trees have been recently proposed in the literature, which use discrete decision variables to model the path each observation will follow in the tree. Instead, we propose a new approach based on continuous optimization. Our classifier can be seen as a randomized tree, since at each node of the decision tree a random decision is made. The computational experience reported demonstrates the good performance of our procedure.

Sparsity in Optimal Randomized Classification Trees

Decision trees are popular Classification and Regression tools and, when small-sized, easy to interpret. Traditionally, a greedy approach has been used to build the trees, yielding a very fast training process; however, controlling sparsity (a proxy for interpretability) is challenging. In recent studies, optimal decision trees, where all decisions are optimized simultaneously, have shown a better learning performance, especially when oblique cuts are implemented. In this paper, we propose a continuous optimization approach to build sparse optimal classification trees, based on oblique cuts, with the aim of using fewer predictor variables in the cuts as well as along the whole tree. Both types of sparsity, namely local and global, are modeled by means of regularizations with polyhedral norms. The computational experience reported supports the usefulness of our methodology. In all our data sets, local and global sparsity can be improved without harming classification accuracy. Unlike greedy approaches, our ability to easily trade in some of our classification accuracy for a gain in global sparsity is shown.