Diana-Nicoleta Grigore
Weight Copy and Low-Rank Adaptation for Few-Shot Distillation of Vision Transformers
Apr 17, 2024
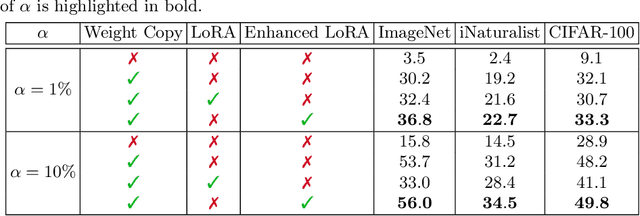


Abstract:Few-shot knowledge distillation recently emerged as a viable approach to harness the knowledge of large-scale pre-trained models, using limited data and computational resources. In this paper, we propose a novel few-shot feature distillation approach for vision transformers. Our approach is based on two key steps. Leveraging the fact that vision transformers have a consistent depth-wise structure, we first copy the weights from intermittent layers of existing pre-trained vision transformers (teachers) into shallower architectures (students), where the intermittence factor controls the complexity of the student transformer with respect to its teacher. Next, we employ an enhanced version of Low-Rank Adaptation (LoRA) to distill knowledge into the student in a few-shot scenario, aiming to recover the information processing carried out by the skipped teacher layers. We present comprehensive experiments with supervised and self-supervised transformers as teachers, on five data sets from various domains, including natural, medical and satellite images. The empirical results confirm the superiority of our approach over competitive baselines. Moreover, the ablation results demonstrate the usefulness of each component of the proposed pipeline.
Discriminability-enforcing loss to improve representation learning
Feb 14, 2022
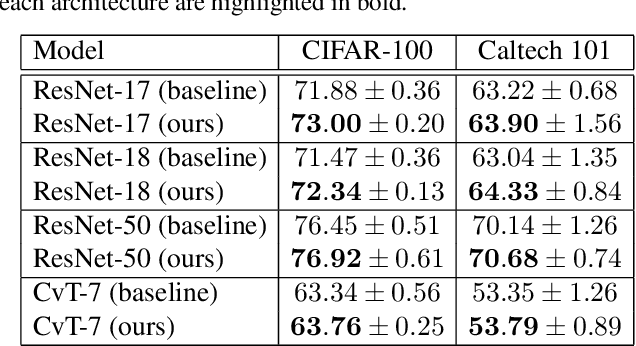
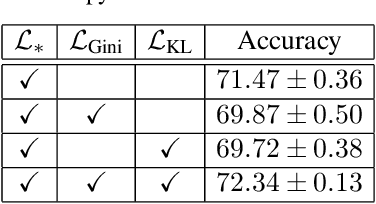
Abstract:During the training process, deep neural networks implicitly learn to represent the input data samples through a hierarchy of features, where the size of the hierarchy is determined by the number of layers. In this paper, we focus on enforcing the discriminative power of the high-level representations, that are typically learned by the deeper layers (closer to the output). To this end, we introduce a new loss term inspired by the Gini impurity, which is aimed at minimizing the entropy (increasing the discriminative power) of individual high-level features with respect to the class labels. Although our Gini loss induces highly-discriminative features, it does not ensure that the distribution of the high-level features matches the distribution of the classes. As such, we introduce another loss term to minimize the Kullback-Leibler divergence between the two distributions. We conduct experiments on two image classification data sets (CIFAR-100 and Caltech 101), considering multiple neural architectures ranging from convolutional networks (ResNet-17, ResNet-18, ResNet-50) to transformers (CvT). Our empirical results show that integrating our novel loss terms into the training objective consistently outperforms the models trained with cross-entropy alone.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge