Discriminability-enforcing loss to improve representation learning

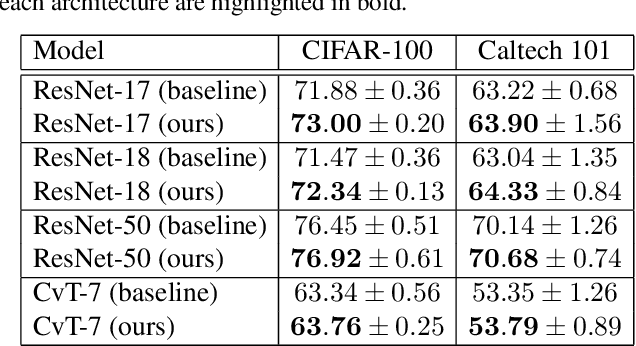
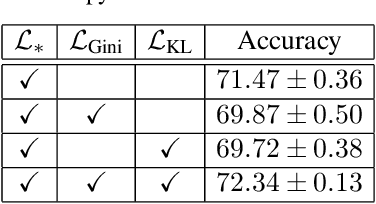
During the training process, deep neural networks implicitly learn to represent the input data samples through a hierarchy of features, where the size of the hierarchy is determined by the number of layers. In this paper, we focus on enforcing the discriminative power of the high-level representations, that are typically learned by the deeper layers (closer to the output). To this end, we introduce a new loss term inspired by the Gini impurity, which is aimed at minimizing the entropy (increasing the discriminative power) of individual high-level features with respect to the class labels. Although our Gini loss induces highly-discriminative features, it does not ensure that the distribution of the high-level features matches the distribution of the classes. As such, we introduce another loss term to minimize the Kullback-Leibler divergence between the two distributions. We conduct experiments on two image classification data sets (CIFAR-100 and Caltech 101), considering multiple neural architectures ranging from convolutional networks (ResNet-17, ResNet-18, ResNet-50) to transformers (CvT). Our empirical results show that integrating our novel loss terms into the training objective consistently outperforms the models trained with cross-entropy alone.