CR-LSO: Convex Neural Architecture Optimization in the Latent Space of Graph Variational Autoencoder with Input Convex Neural Networks

In neural architecture search (NAS) methods based on latent space optimization (LSO), a deep generative model is trained to embed discrete neural architectures into a continuous latent space. In this case, different optimization algorithms that operate in the continuous space can be implemented to search neural architectures. However, the optimization of latent variables is challenging for gradient-based LSO since the mapping from the latent space to the architecture performance is generally non-convex. To tackle this problem, this paper develops a convexity regularized latent space optimization (CR-LSO) method, which aims to regularize the learning process of latent space in order to obtain a convex architecture performance mapping. Specifically, CR-LSO trains a graph variational autoencoder (G-VAE) to learn the continuous representations of discrete architectures. Simultaneously, the learning process of latent space is regularized by the guaranteed convexity of input convex neural networks (ICNNs). In this way, the G-VAE is forced to learn a convex mapping from the architecture representation to the architecture performance. Hereafter, the CR-LSO approximates the performance mapping using the ICNN and leverages the estimated gradient to optimize neural architecture representations. Experimental results on three popular NAS benchmarks show that CR-LSO achieves competitive evaluation results in terms of both computational complexity and architecture performance.

Q-learning for Optimal Control of Continuous-time Systems

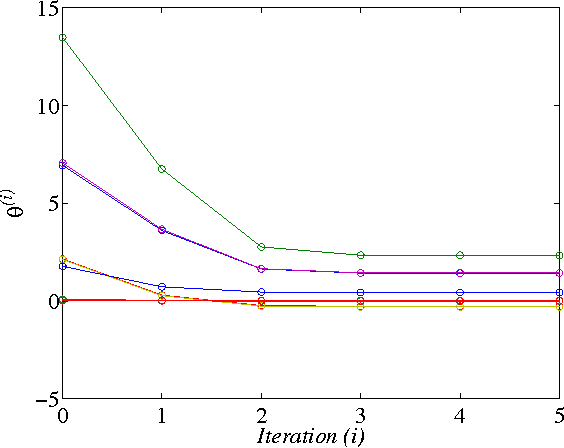
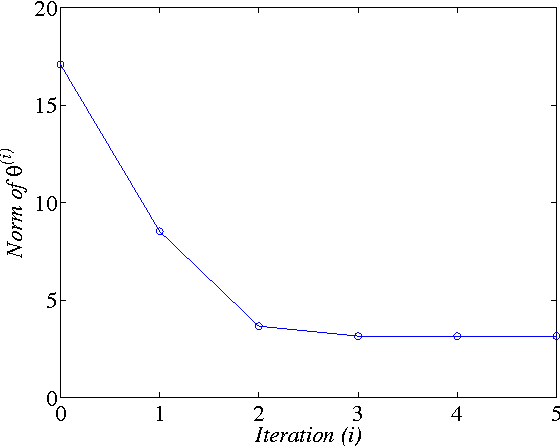
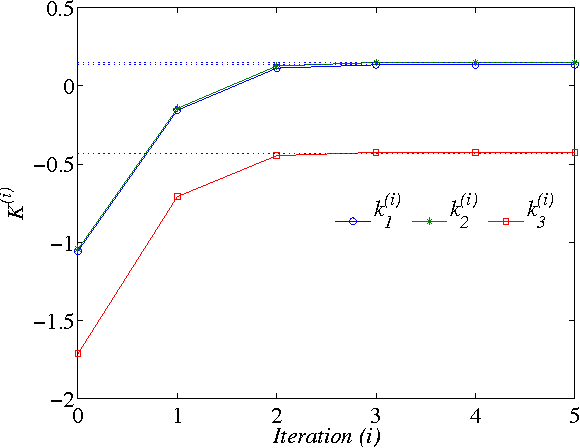
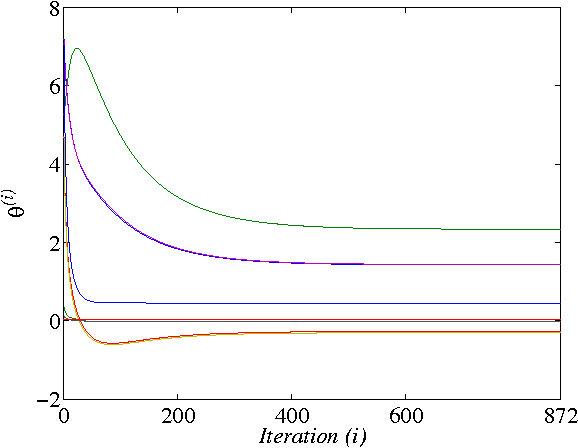
In this paper, two Q-learning (QL) methods are proposed and their convergence theories are established for addressing the model-free optimal control problem of general nonlinear continuous-time systems. By introducing the Q-function for continuous-time systems, policy iteration based QL (PIQL) and value iteration based QL (VIQL) algorithms are proposed for learning the optimal control policy from real system data rather than using mathematical system model. It is proved that both PIQL and VIQL methods generate a nonincreasing Q-function sequence, which converges to the optimal Q-function. For implementation of the QL algorithms, the method of weighted residuals is applied to derived the parameters update rule. The developed PIQL and VIQL algorithms are essentially off-policy reinforcement learning approachs, where the system data can be collected arbitrary and thus the exploration ability is increased. With the data collected from the real system, the QL methods learn the optimal control policy offline, and then the convergent control policy will be employed to real system. The effectiveness of the developed QL algorithms are verified through computer simulation.

Data-based approximate policy iteration for nonlinear continuous-time optimal control design

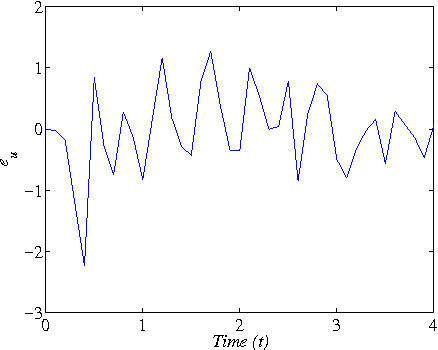
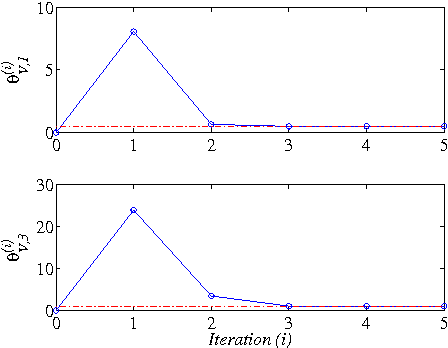
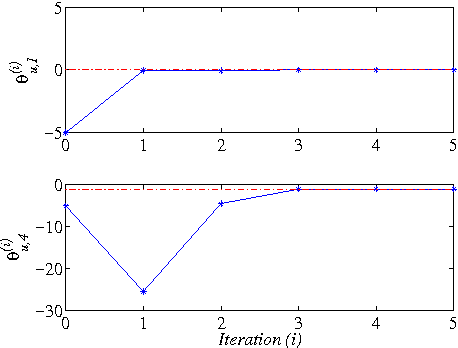
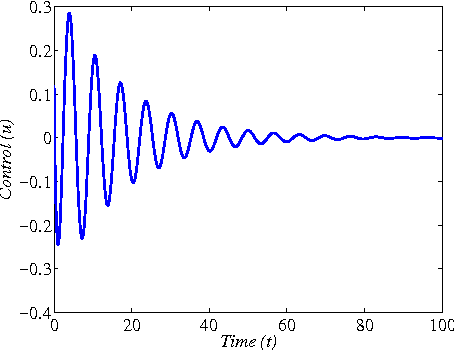
This paper addresses the model-free nonlinear optimal problem with generalized cost functional, and a data-based reinforcement learning technique is developed. It is known that the nonlinear optimal control problem relies on the solution of the Hamilton-Jacobi-Bellman (HJB) equation, which is a nonlinear partial differential equation that is generally impossible to be solved analytically. Even worse, most of practical systems are too complicated to establish their accurate mathematical model. To overcome these difficulties, we propose a data-based approximate policy iteration (API) method by using real system data rather than system model. Firstly, a model-free policy iteration algorithm is derived for constrained optimal control problem and its convergence is proved, which can learn the solution of HJB equation and optimal control policy without requiring any knowledge of system mathematical model. The implementation of the algorithm is based on the thought of actor-critic structure, where actor and critic neural networks (NNs) are employed to approximate the control policy and cost function, respectively. To update the weights of actor and critic NNs, a least-square approach is developed based on the method of weighted residuals. The whole data-based API method includes two parts, where the first part is implemented online to collect real system information, and the second part is conducting offline policy iteration to learn the solution of HJB equation and the control policy. Then, the data-based API algorithm is simplified for solving unconstrained optimal control problem of nonlinear and linear systems. Finally, we test the efficiency of the data-based API control design method on a simple nonlinear system, and further apply it to a rotational/translational actuator system. The simulation results demonstrate the effectiveness of the proposed method.