Q-learning for Optimal Control of Continuous-time Systems

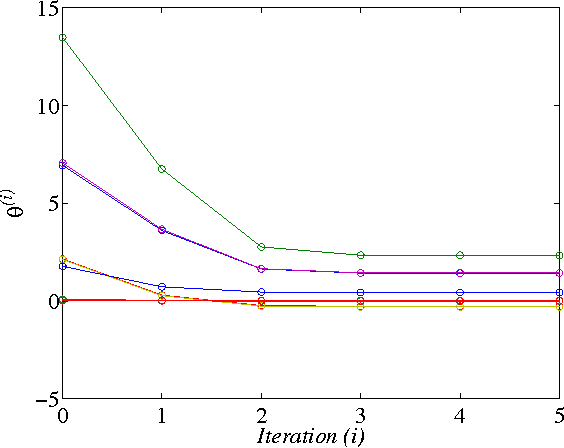
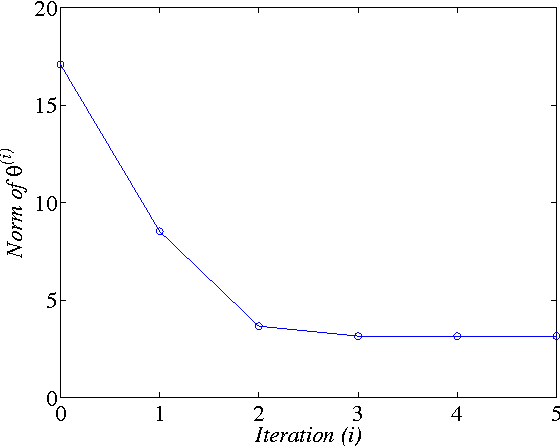
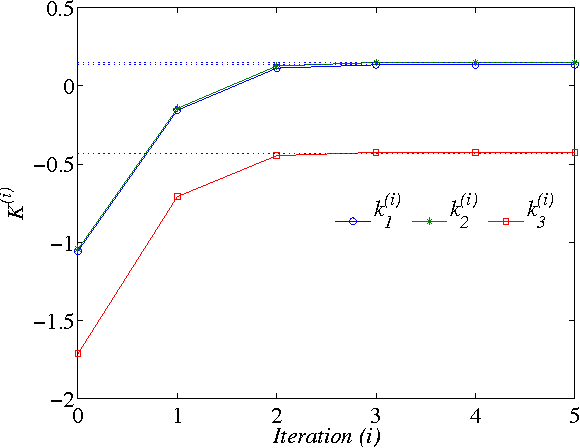
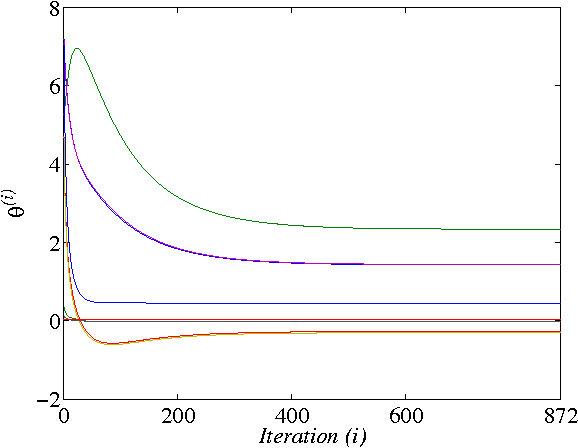
In this paper, two Q-learning (QL) methods are proposed and their convergence theories are established for addressing the model-free optimal control problem of general nonlinear continuous-time systems. By introducing the Q-function for continuous-time systems, policy iteration based QL (PIQL) and value iteration based QL (VIQL) algorithms are proposed for learning the optimal control policy from real system data rather than using mathematical system model. It is proved that both PIQL and VIQL methods generate a nonincreasing Q-function sequence, which converges to the optimal Q-function. For implementation of the QL algorithms, the method of weighted residuals is applied to derived the parameters update rule. The developed PIQL and VIQL algorithms are essentially off-policy reinforcement learning approachs, where the system data can be collected arbitrary and thus the exploration ability is increased. With the data collected from the real system, the QL methods learn the optimal control policy offline, and then the convergent control policy will be employed to real system. The effectiveness of the developed QL algorithms are verified through computer simulation.