Debjani Bhowmick
Improving Solar Cell Metallization Designs using Convolutional Neural Networks
Apr 08, 2021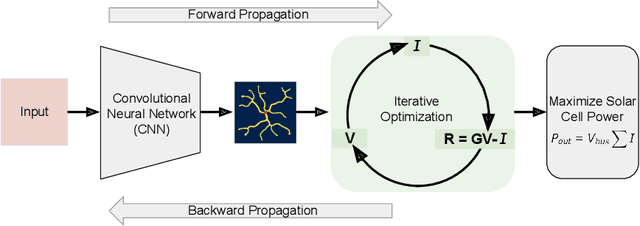
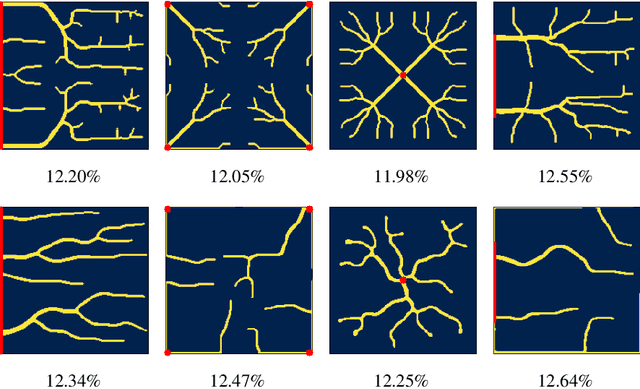
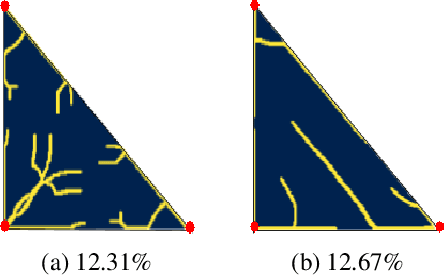
Abstract:Optimizing the design of solar cell metallizations is one of the ways to improve the performance of solar cells. Recently, it has been shown that Topology Optimization (TO) can be used to design complex metallization patterns for solar cells that lead to improved performance. TO generates unconventional design patterns that cannot be obtained with the traditional shape optimization methods. In this paper, we show that this design process can be improved further using a deep learning inspired strategy. We present SolarNet, a CNN-based reparameterization scheme that can be used to obtain improved metallization designs. SolarNet modifies the optimization domain such that rather than optimizing the electrode material distribution directly, the weights of a CNN model are optimized. The design generated by CNN is then evaluated using the physics equations, which in turn generates gradients for backpropagation. SolarNet is trained end-to-end involving backpropagation through the solar cell model as well as the CNN pipeline. Through application on solar cells of different shapes as well as different busbar geometries, we demonstrate that SolarNet improves the performance of solar cells compared to the traditional TO approach.
Applying Knowledge Transfer for Water Body Segmentation in Peru
Dec 02, 2019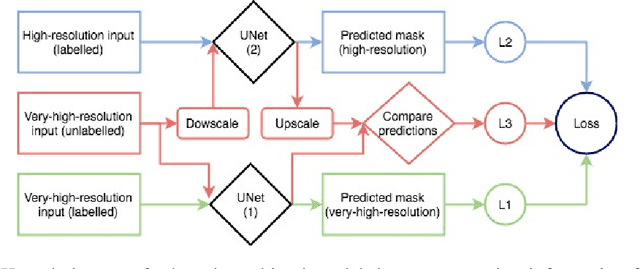
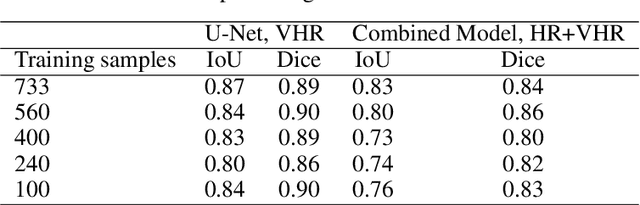
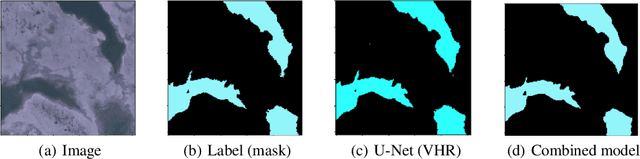
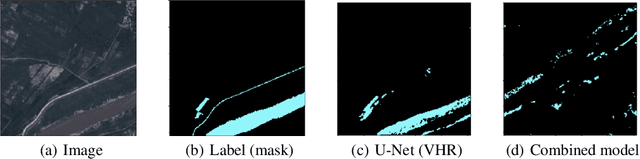
Abstract:In this work, we present the application of convolutional neural networks for segmenting water bodies in satellite images. We first use a variant of the U-Net model to segment rivers and lakes from very high-resolution images from Peru. To circumvent the issue of scarce labelled data, we investigate the applicability of a knowledge transfer-based model that learns the mapping from high-resolution labelled images and combines it with the very high-resolution mapping so that better segmentation can be achieved. We train this model in a single process, end-to-end. Our preliminary results show that adding the information from the available high-resolution images does not help out-of-the-box, and in fact worsen results. This leads us to infer that the high-resolution data could be from a different distribution, and its addition leads to increased variance in our results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge