David P. Hofmeyr
Nearest Neighbour Equilibrium Clustering
Mar 27, 2025Abstract:A novel and intuitive nearest neighbours based clustering algorithm is introduced, in which a cluster is defined in terms of an equilibrium condition which balances its size and cohesiveness. The formulation of the equilibrium condition allows for a quantification of the strength of alignment of each point to a cluster, with these cluster alignment strengths leading naturally to a model selection criterion which renders the proposed approach fully automatable. The algorithm is simple to implement and computationally efficient, and produces clustering solutions of extremely high quality in comparison with relevant benchmarks from the literature. R code to implement the approach is available from https://github.com/DavidHofmeyr/NNEC.
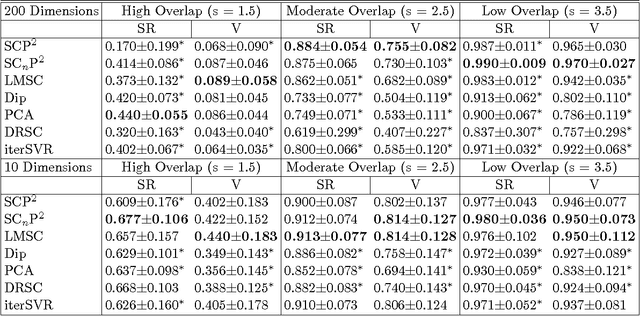
Bags of Projected Nearest Neighbours: Competitors to Random Forests?
Mar 12, 2025Abstract:In this paper we introduce a simple and intuitive adaptive k nearest neighbours classifier, and explore its utility within the context of bootstrap aggregating ("bagging"). The approach is based on finding discriminant subspaces which are computationally efficient to compute, and are motivated by enhancing the discrimination of classes through nearest neighbour classifiers. This adaptiveness promotes diversity of the individual classifiers fit across different bootstrap samples, and so further leverages the variance reducing effect of bagging. Extensive experimental results are presented documenting the strong performance of the proposed approach in comparison with Random Forest classifiers, as well as other nearest neighbours based ensembles from the literature, plus other relevant benchmarks. Code to implement the proposed approach is available in the form of an R package from https://github.com/DavidHofmeyr/BOPNN.
Clustering by Nonparametric Smoothing
Mar 12, 2025Abstract:A novel formulation of the clustering problem is introduced in which the task is expressed as an estimation problem, where the object to be estimated is a function which maps a point to its distribution of cluster membership. Unlike existing approaches which implicitly estimate such a function, like Gaussian Mixture Models (GMMs), the proposed approach bypasses any explicit modelling assumptions and exploits the flexible estimation potential of nonparametric smoothing. An intuitive approach for selecting the tuning parameters governing estimation is provided, which allows the proposed method to automatically determine both an appropriate level of flexibility and also the number of clusters to extract from a given data set. Experiments on a large collection of publicly available data sets are used to document the strong performance of the proposed approach, in comparison with relevant benchmarks from the literature. R code to implement the proposed approach is available from https://github.com/DavidHofmeyr/ CNS
Optimal Projections for Classification with Naive Bayes
Sep 09, 2024Abstract:In the Naive Bayes classification model the class conditional densities are estimated as the products of their marginal densities along the cardinal basis directions. We study the problem of obtaining an alternative basis for this factorisation with the objective of enhancing the discriminatory power of the associated classification model. We formulate the problem as a projection pursuit to find the optimal linear projection on which to perform classification. Optimality is determined based on the multinomial likelihood within which probabilities are estimated using the Naive Bayes factorisation of the projected data. Projection pursuit offers the added benefits of dimension reduction and visualisation. We discuss an intuitive connection with class conditional independent components analysis, and show how this is realised visually in practical applications. The performance of the resulting classification models is investigated using a large collection of (162) publicly available benchmark data sets and in comparison with relevant alternatives. We find that the proposed approach substantially outperforms other popular probabilistic discriminant analysis models and is highly competitive with Support Vector Machines.
Clustering Large Data Sets with Incremental Estimation of Low-density Separating Hyperplanes
Aug 07, 2021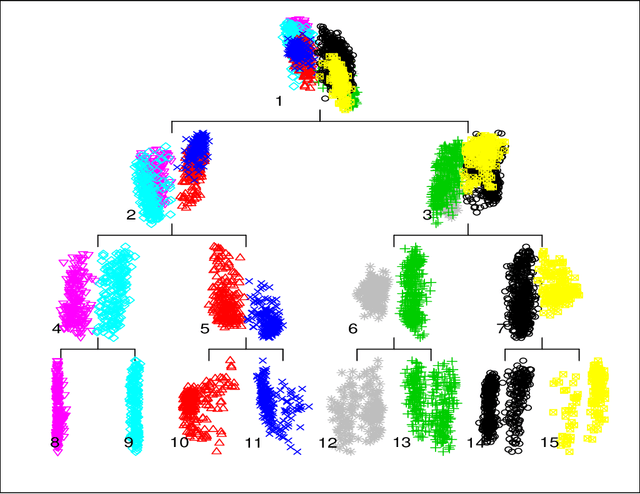
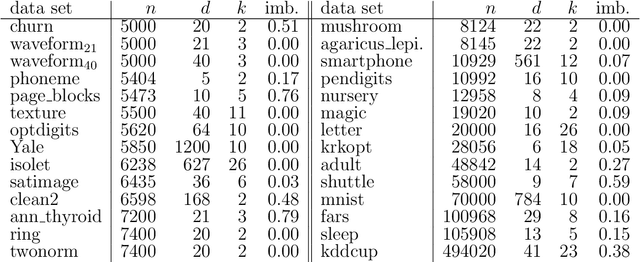
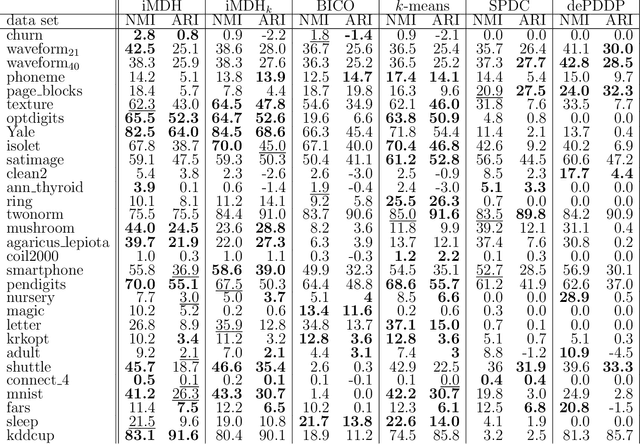
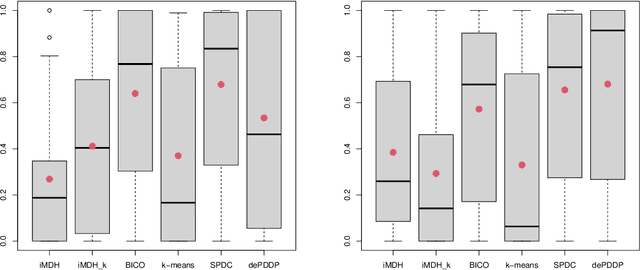
Abstract:An efficient method for obtaining low-density hyperplane separators in the unsupervised context is proposed. Low density separators can be used to obtain a partition of a set of data based on their allocations to the different sides of the separators. The proposed method is based on applying stochastic gradient descent to the integrated density on the hyperplane with respect to a convolution of the underlying distribution and a smoothing kernel. In the case where the bandwidth of the smoothing kernel is decreased towards zero, the bias of these updates with respect to the true underlying density tends to zero, and convergence to a minimiser of the density on the hyperplane can be obtained. A post-processing of the partition induced by a collection of low-density hyperplanes yields an efficient and accurate clustering method which is capable of automatically selecting an appropriate number of clusters. Experiments with the proposed approach show that it is highly competitive in terms of both speed and accuracy when compared with relevant benchmarks. Code to implement the proposed approach is available in the form of an R package from https://github.com/DavidHofmeyr/iMDH.
Connecting Spectral Clustering to Maximum Margins and Level Sets
Dec 16, 2018Abstract:We study the connections between spectral clustering and the problems of maximum margin clustering, and estimation of the components of level sets of a density function. Specifically, we obtain bounds on the eigenvectors of graph Laplacian matrices in terms of the between cluster separation, and within cluster connectivity. These bounds ensure that the spectral clustering solution converges to the maximum margin clustering solution as the scaling parameter is reduced towards zero. The sensitivity of maximum margin clustering solutions to outlying points is well known, but can be mitigated by first removing such outliers, and applying maximum margin clustering to the remaining points. If outliers are identified using an estimate of the underlying probability density, then the remaining points may be seen as an estimate of a level set of this density function. We show that such an approach can be used to consistently estimate the components of the level sets of a density function under very mild assumptions.
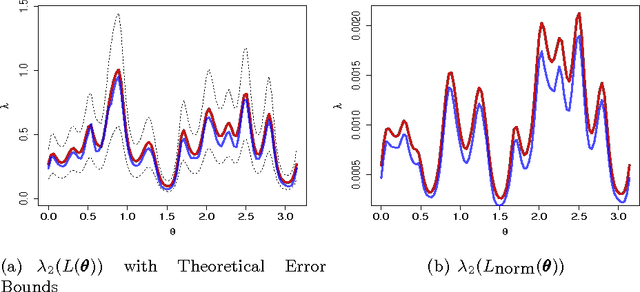
Degrees of Freedom and Model Selection for kmeans Clustering
Jul 28, 2018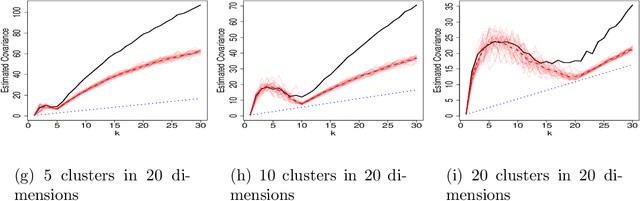

Abstract:This paper investigates the problem of model selection for kmeans clustering, based on conservative estimates of the model degrees of freedom. An extension of Stein's lemma, which is used in unbiased risk estimation, is used to obtain an expression which allows one to approximate the degrees of freedom. Empirically based estimates of this approximation are obtained. The degrees of freedom estimates are then used within the popular Bayesian Information Criterion to perform model selection. The proposed estimation procedure is validated in a thorough simulation study, and the robustness is assessed through relaxations of the modelling assumptions and on data from real applications. Comparisons with popular existing techniques suggest that this approach performs extremely well when the modelling assumptions
Minimum Spectral Connectivity Projection Pursuit
Nov 13, 2017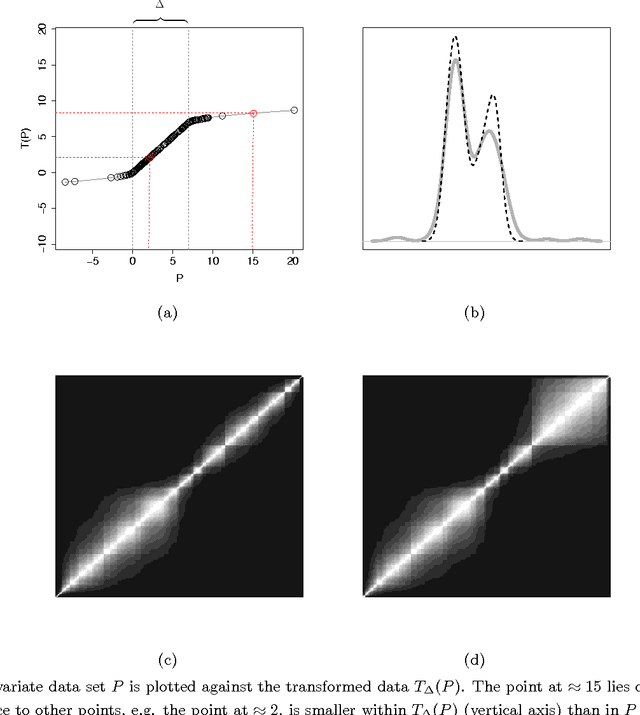
Abstract:We study the problem of determining the optimal low dimensional projection for maximising the separability of a binary partition of an unlabelled dataset, as measured by spectral graph theory. This is achieved by finding projections which minimise the second eigenvalue of the graph Laplacian of the projected data, which corresponds to a non-convex, non-smooth optimisation problem. We show that the optimal univariate projection based on spectral connectivity converges to the vector normal to the maximum margin hyperplane through the data, as the scaling parameter is reduced to zero. This establishes a connection between connectivity as measured by spectral graph theory and maximal Euclidean separation. The computational cost associated with each eigen-problem is quadratic in the number of data. To mitigate this issue, we propose an approximation method using microclusters with provable approximation error bounds. Combining multiple binary partitions within a divisive hierarchical model allows us to construct clustering solutions admitting clusters with varying scales and lying within different subspaces. We evaluate the performance of the proposed method on a large collection of benchmark datasets and find that it compares favourably with existing methods for projection pursuit and dimension reduction for data clustering.
Minimum Density Hyperplanes
Sep 28, 2016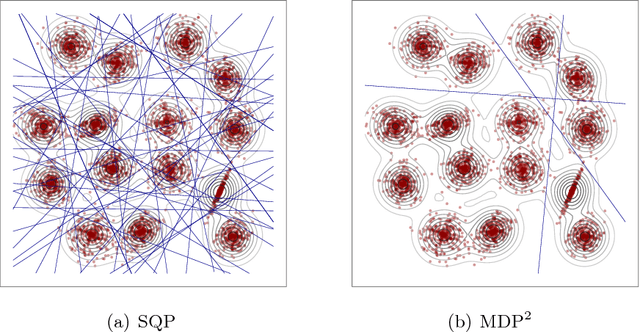



Abstract:Associating distinct groups of objects (clusters) with contiguous regions of high probability density (high-density clusters), is central to many statistical and machine learning approaches to the classification of unlabelled data. We propose a novel hyperplane classifier for clustering and semi-supervised classification which is motivated by this objective. The proposed minimum density hyperplane minimises the integral of the empirical probability density function along it, thereby avoiding intersection with high density clusters. We show that the minimum density and the maximum margin hyperplanes are asymptotically equivalent, thus linking this approach to maximum margin clustering and semi-supervised support vector classifiers. We propose a projection pursuit formulation of the associated optimisation problem which allows us to find minimum density hyperplanes efficiently in practice, and evaluate its performance on a range of benchmark datasets. The proposed approach is found to be very competitive with state of the art methods for clustering and semi-supervised classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge