Innovative And Additive Outlier Robust Kalman Filtering With A Robust Particle Filter

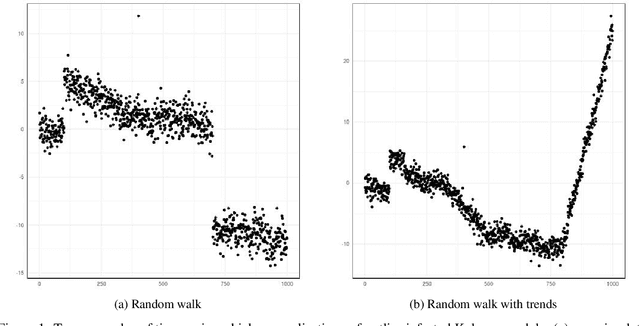
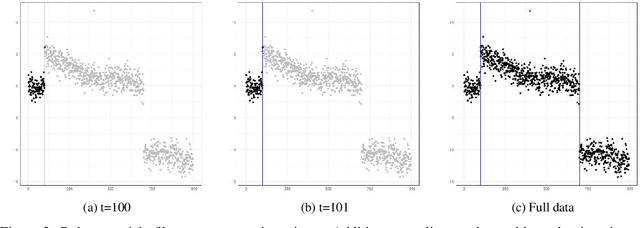
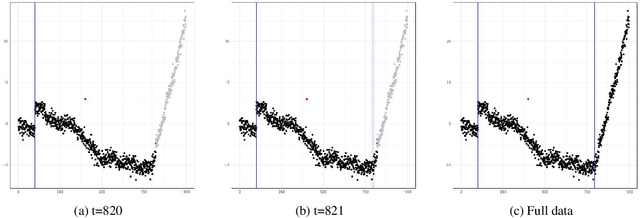
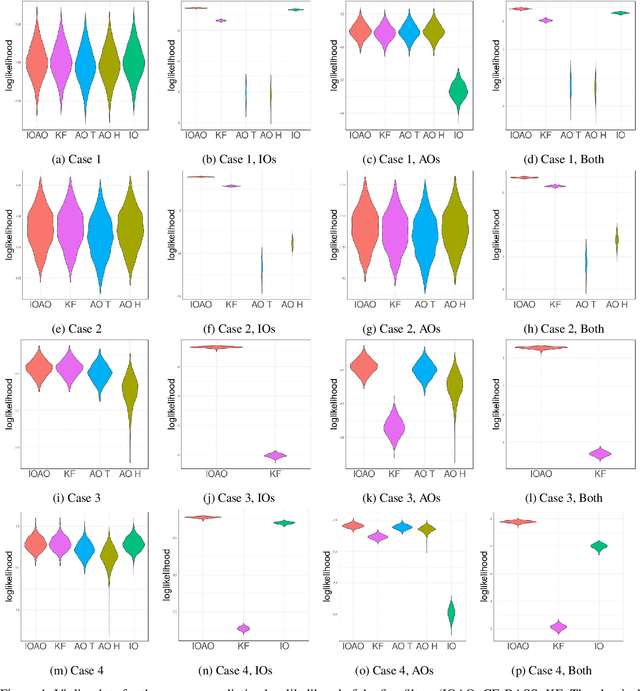
In this paper, we propose CE-BASS, a particle mixture Kalman filter which is robust to both innovative and additive outliers, and able to fully capture multi-modality in the distribution of the hidden state. Furthermore, the particle sampling approach re-samples past states, which enables CE-BASS to handle innovative outliers which are not immediately visible in the observations, such as trend changes. The filter is computationally efficient as we derive new, accurate approximations to the optimal proposal distributions for the particles. The proposed algorithm is shown to compare well with existing approaches and is applied to both machine temperature and server data.

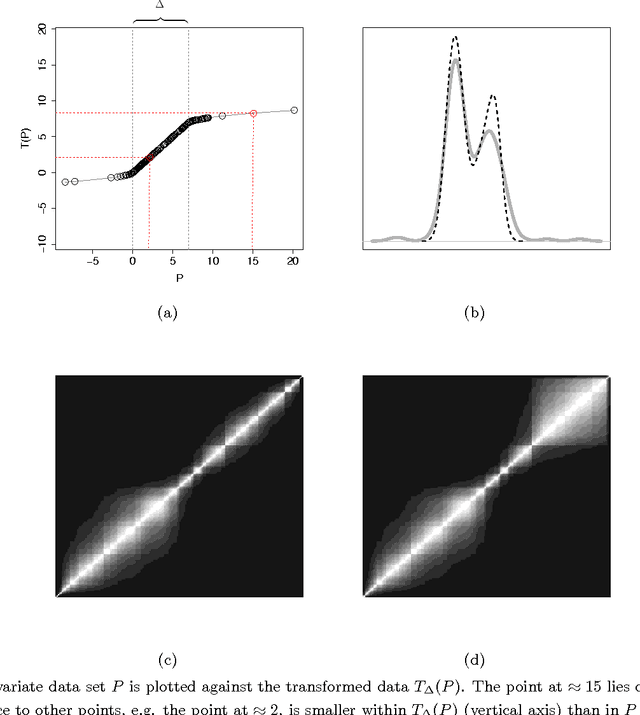
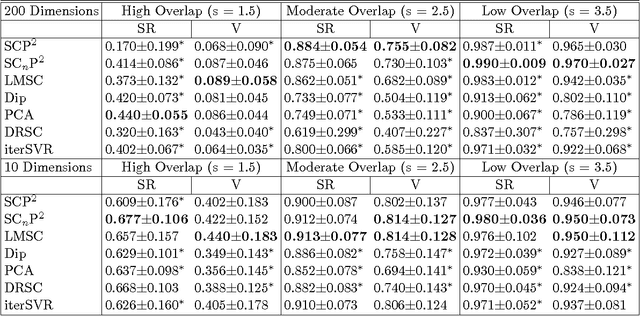
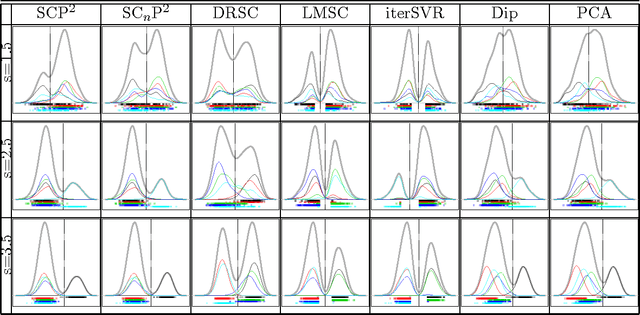
Minimum Spectral Connectivity Projection Pursuit

We study the problem of determining the optimal low dimensional projection for maximising the separability of a binary partition of an unlabelled dataset, as measured by spectral graph theory. This is achieved by finding projections which minimise the second eigenvalue of the graph Laplacian of the projected data, which corresponds to a non-convex, non-smooth optimisation problem. We show that the optimal univariate projection based on spectral connectivity converges to the vector normal to the maximum margin hyperplane through the data, as the scaling parameter is reduced to zero. This establishes a connection between connectivity as measured by spectral graph theory and maximal Euclidean separation. The computational cost associated with each eigen-problem is quadratic in the number of data. To mitigate this issue, we propose an approximation method using microclusters with provable approximation error bounds. Combining multiple binary partitions within a divisive hierarchical model allows us to construct clustering solutions admitting clusters with varying scales and lying within different subspaces. We evaluate the performance of the proposed method on a large collection of benchmark datasets and find that it compares favourably with existing methods for projection pursuit and dimension reduction for data clustering.

Efficient penalty search for multiple changepoint problems

In the multiple changepoint setting, various search methods have been proposed which involve optimising either a constrained or penalised cost function over possible numbers and locations of changepoints using dynamic programming. Such methods are typically computationally intensive. Recent work in the penalised optimisation setting has focussed on developing a pruning-based approach which gives an improved computational cost that, under certain conditions, is linear in the number of data points. Such an approach naturally requires the specification of a penalty to avoid under/over-fitting. Work has been undertaken to identify the appropriate penalty choice for data generating processes with known distributional form, but in many applications the model assumed for the data is not correct and these penalty choices are not always appropriate. Consequently it is desirable to have an approach that enables us to compare segmentations for different choices of penalty. To this end we present a method to obtain optimal changepoint segmentations of data sequences for all penalty values across a continuous range. This permits an evaluation of the various segmentations to identify a suitably parsimonious penalty choice. The computational complexity of this approach can be linear in the number of data points and linear in the difference between the number of changepoints in the optimal segmentations for the smallest and largest penalty values. This can be orders of magnitude faster than alternative approaches that find optimal segmentations for a range of the number of changepoints.