Weighted Sparse Subspace Representation: A Unified Framework for Subspace Clustering, Constrained Clustering, and Active Learning

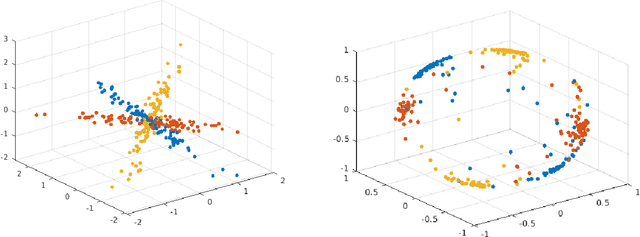
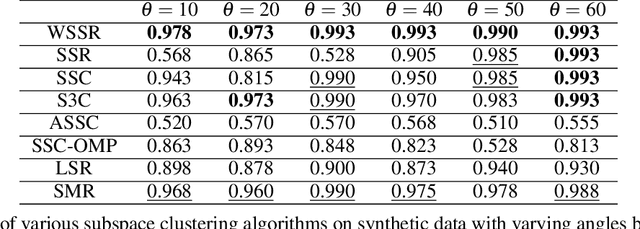
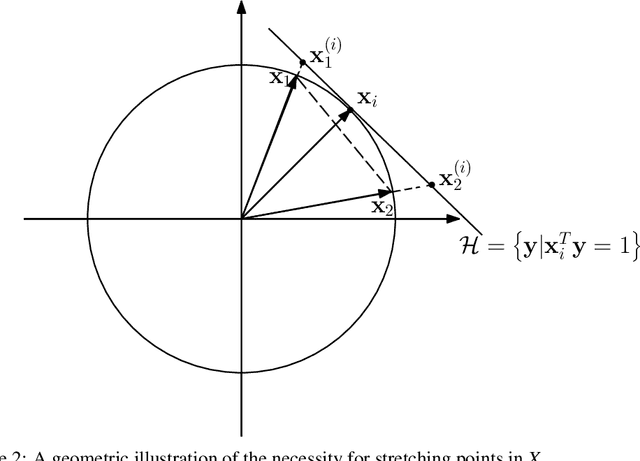
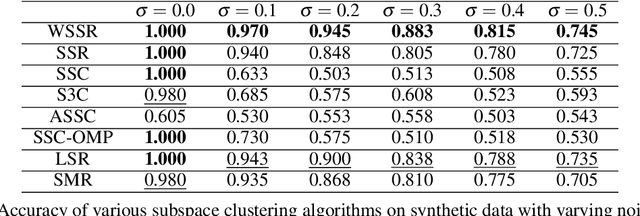
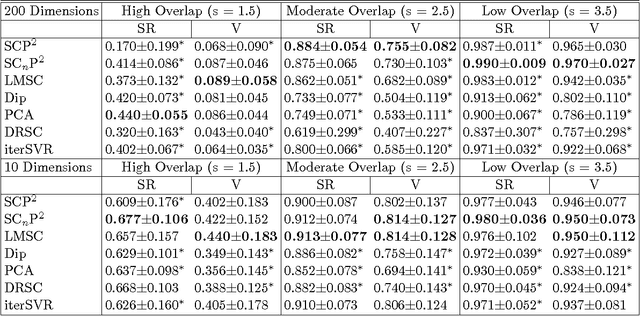
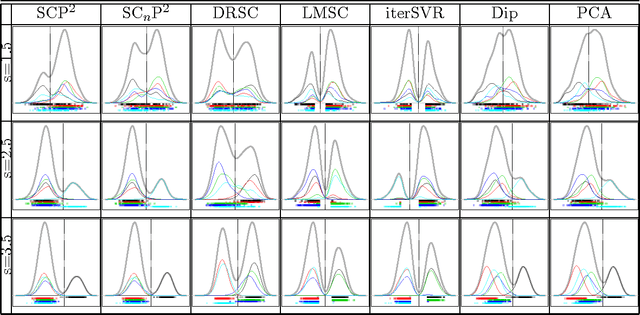
Spectral-based subspace clustering methods have proved successful in many challenging applications such as gene sequencing, image recognition, and motion segmentation. In this work, we first propose a novel spectral-based subspace clustering algorithm that seeks to represent each point as a sparse convex combination of a few nearby points. We then extend the algorithm to constrained clustering and active learning settings. Our motivation for developing such a framework stems from the fact that typically either a small amount of labelled data is available in advance; or it is possible to label some points at a cost. The latter scenario is typically encountered in the process of validating a cluster assignment. Extensive experiments on simulated and real data sets show that the proposed approach is effective and competitive with state-of-the-art methods.

Subspace Clustering with Active Learning

Subspace clustering is a growing field of unsupervised learning that has gained much popularity in the computer vision community. Applications can be found in areas such as motion segmentation and face clustering. It assumes that data originate from a union of subspaces, and clusters the data depending on the corresponding subspace. In practice, it is reasonable to assume that a limited amount of labels can be obtained, potentially at a cost. Therefore, algorithms that can effectively and efficiently incorporate this information to improve the clustering model are desirable. In this paper, we propose an active learning framework for subspace clustering that sequentially queries informative points and updates the subspace model. The query stage of the proposed framework relies on results from the perturbation theory of principal component analysis, to identify influential and potentially misclassified points. A constrained subspace clustering algorithm is proposed that monotonically decreases the objective function subject to the constraints imposed by the labelled data. We show that our proposed framework is suitable for subspace clustering algorithms including iterative methods and spectral methods. Experiments on synthetic data sets, motion segmentation data sets, and Yale Faces data sets demonstrate the advantage of our proposed active strategy over state-of-the-art.

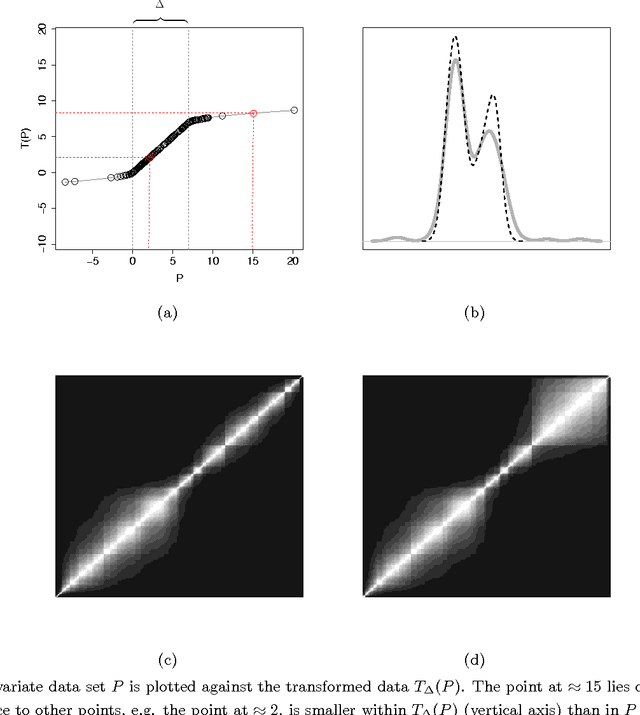
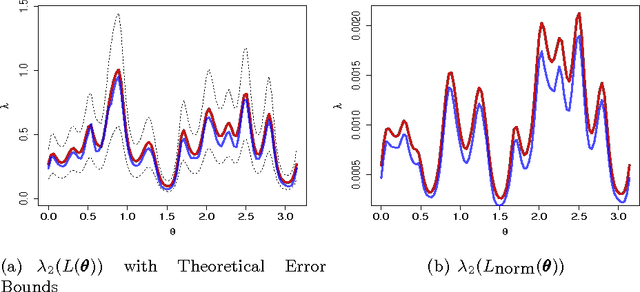
Minimum Spectral Connectivity Projection Pursuit

We study the problem of determining the optimal low dimensional projection for maximising the separability of a binary partition of an unlabelled dataset, as measured by spectral graph theory. This is achieved by finding projections which minimise the second eigenvalue of the graph Laplacian of the projected data, which corresponds to a non-convex, non-smooth optimisation problem. We show that the optimal univariate projection based on spectral connectivity converges to the vector normal to the maximum margin hyperplane through the data, as the scaling parameter is reduced to zero. This establishes a connection between connectivity as measured by spectral graph theory and maximal Euclidean separation. The computational cost associated with each eigen-problem is quadratic in the number of data. To mitigate this issue, we propose an approximation method using microclusters with provable approximation error bounds. Combining multiple binary partitions within a divisive hierarchical model allows us to construct clustering solutions admitting clusters with varying scales and lying within different subspaces. We evaluate the performance of the proposed method on a large collection of benchmark datasets and find that it compares favourably with existing methods for projection pursuit and dimension reduction for data clustering.

Minimum Density Hyperplanes

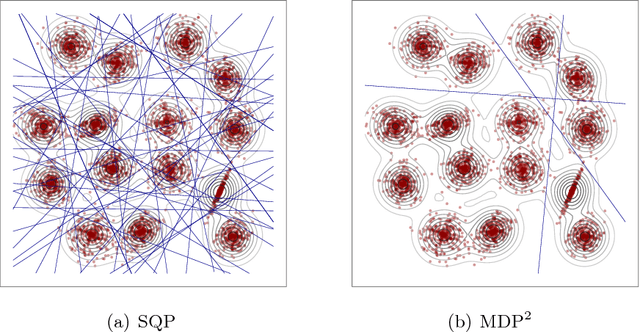
Associating distinct groups of objects (clusters) with contiguous regions of high probability density (high-density clusters), is central to many statistical and machine learning approaches to the classification of unlabelled data. We propose a novel hyperplane classifier for clustering and semi-supervised classification which is motivated by this objective. The proposed minimum density hyperplane minimises the integral of the empirical probability density function along it, thereby avoiding intersection with high density clusters. We show that the minimum density and the maximum margin hyperplanes are asymptotically equivalent, thus linking this approach to maximum margin clustering and semi-supervised support vector classifiers. We propose a projection pursuit formulation of the associated optimisation problem which allows us to find minimum density hyperplanes efficiently in practice, and evaluate its performance on a range of benchmark datasets. The proposed approach is found to be very competitive with state of the art methods for clustering and semi-supervised classification.