Subspace Change-Point Detection via Low-Rank Matrix Factorisation

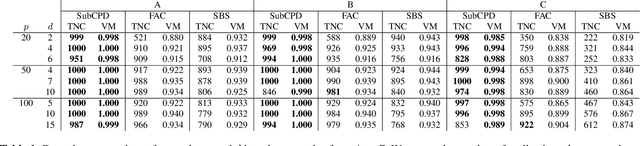
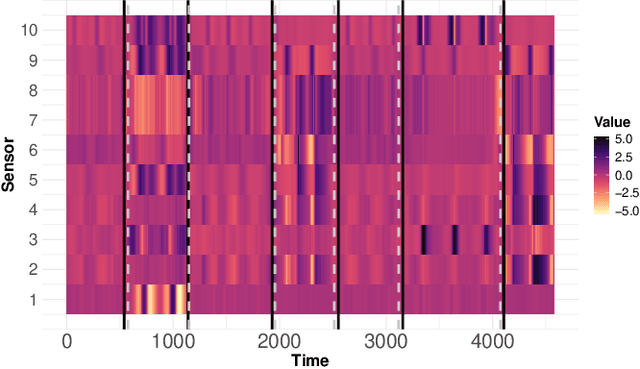
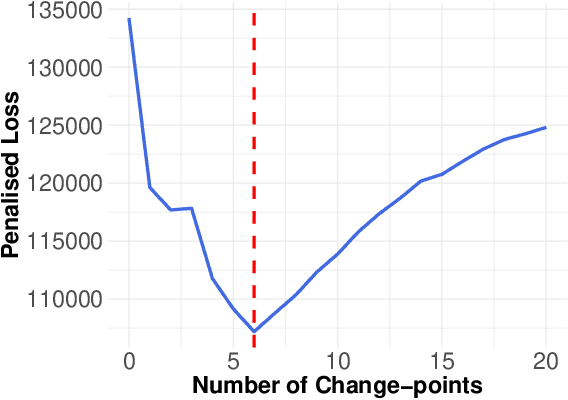
Multivariate time series can often have a large number of dimensions, whether it is due to the vast amount of collected features or due to how the data sources are processed. Frequently, the main structure of the high-dimensional time series can be well represented by a lower dimensional subspace. As vast quantities of data are being collected over long periods of time, it is reasonable to assume that the underlying subspace structure would change over time. In this work, we propose a change-point detection method based on low-rank matrix factorisation that can detect multiple changes in the underlying subspace of a multivariate time series. Experimental results on both synthetic and real data sets demonstrate the effectiveness of our approach and its advantages against various state-of-the-art methods.

Weighted Sparse Subspace Representation: A Unified Framework for Subspace Clustering, Constrained Clustering, and Active Learning

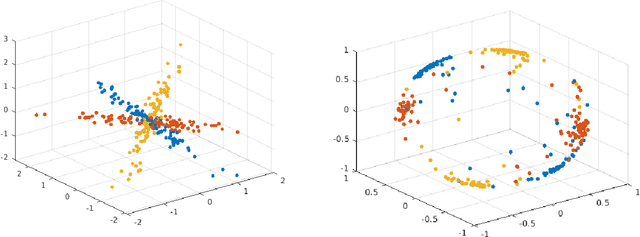
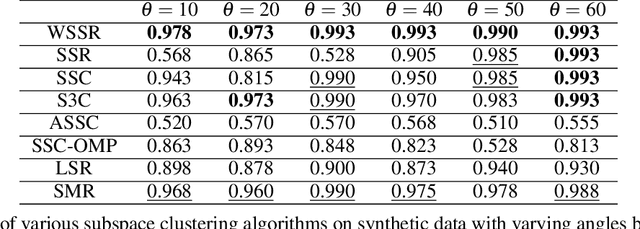
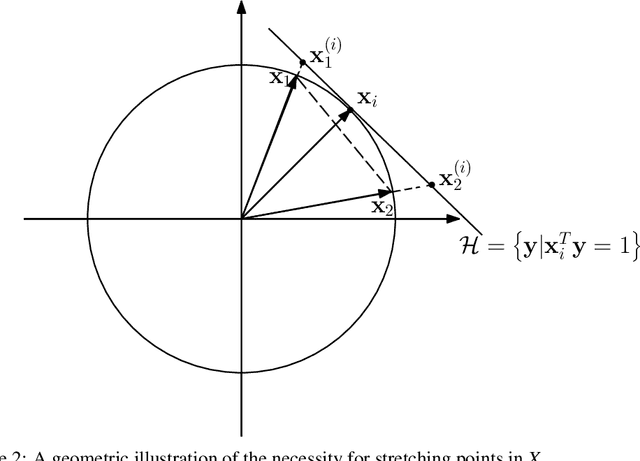
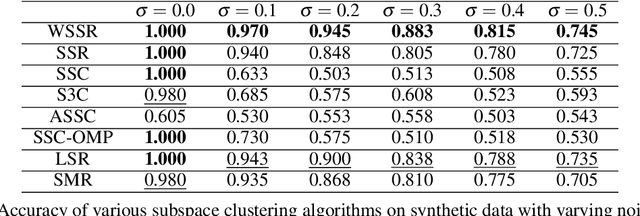
Spectral-based subspace clustering methods have proved successful in many challenging applications such as gene sequencing, image recognition, and motion segmentation. In this work, we first propose a novel spectral-based subspace clustering algorithm that seeks to represent each point as a sparse convex combination of a few nearby points. We then extend the algorithm to constrained clustering and active learning settings. Our motivation for developing such a framework stems from the fact that typically either a small amount of labelled data is available in advance; or it is possible to label some points at a cost. The latter scenario is typically encountered in the process of validating a cluster assignment. Extensive experiments on simulated and real data sets show that the proposed approach is effective and competitive with state-of-the-art methods.

HERS Superpixels: Deep Affinity Learning for Hierarchical Entropy Rate Segmentation

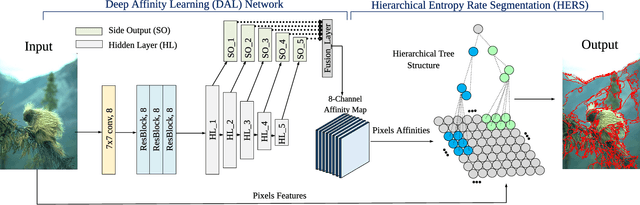
Superpixels serve as a powerful preprocessing tool in many computer vision tasks. By using superpixel representation, the number of image primitives can be largely reduced by orders of magnitudes. The majority of superpixel methods use handcrafted features, which usually do not translate well into strong adherence to object boundaries. A few recent superpixel methods have introduced deep learning into the superpixel segmentation process. However, none of these methods is able to produce superpixels in near real-time, which is crucial to the applicability of a superpixel method in practice. In this work, we propose a two-stage graph-based framework for superpixel segmentation. In the first stage, we introduce an efficient Deep Affinity Learning (DAL) network that learns pairwise pixel affinities by aggregating multi-scale information. In the second stage, we propose a highly efficient superpixel method called Hierarchical Entropy Rate Segmentation (HERS). Using the learned affinities from the first stage, HERS builds a hierarchical tree structure that can produce any number of highly adaptive superpixels instantaneously. We demonstrate, through visual and numerical experiments, the effectiveness and efficiency of our method compared to various state-of-the-art superpixel methods.

Subspace Clustering with Active Learning

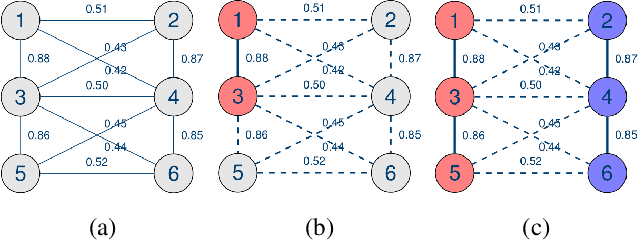
Subspace clustering is a growing field of unsupervised learning that has gained much popularity in the computer vision community. Applications can be found in areas such as motion segmentation and face clustering. It assumes that data originate from a union of subspaces, and clusters the data depending on the corresponding subspace. In practice, it is reasonable to assume that a limited amount of labels can be obtained, potentially at a cost. Therefore, algorithms that can effectively and efficiently incorporate this information to improve the clustering model are desirable. In this paper, we propose an active learning framework for subspace clustering that sequentially queries informative points and updates the subspace model. The query stage of the proposed framework relies on results from the perturbation theory of principal component analysis, to identify influential and potentially misclassified points. A constrained subspace clustering algorithm is proposed that monotonically decreases the objective function subject to the constraints imposed by the labelled data. We show that our proposed framework is suitable for subspace clustering algorithms including iterative methods and spectral methods. Experiments on synthetic data sets, motion segmentation data sets, and Yale Faces data sets demonstrate the advantage of our proposed active strategy over state-of-the-art.

Subspace Clustering of Very Sparse High-Dimensional Data

In this paper we consider the problem of clustering collections of very short texts using subspace clustering. This problem arises in many applications such as product categorisation, fraud detection, and sentiment analysis. The main challenge lies in the fact that the vectorial representation of short texts is both high-dimensional, due to the large number of unique terms in the corpus, and extremely sparse, as each text contains a very small number of words with no repetition. We propose a new, simple subspace clustering algorithm that relies on linear algebra to cluster such datasets. Experimental results on identifying product categories from product names obtained from the US Amazon website indicate that the algorithm can be competitive against state-of-the-art clustering algorithms.