Diffusion Generative Modelling for Divide-and-Conquer MCMC

Divide-and-conquer MCMC is a strategy for parallelising Markov Chain Monte Carlo sampling by running independent samplers on disjoint subsets of a dataset and merging their output. An ongoing challenge in the literature is to efficiently perform this merging without imposing distributional assumptions on the posteriors. We propose using diffusion generative modelling to fit density approximations to the subposterior distributions. This approach outperforms existing methods on challenging merging problems, while its computational cost scales more efficiently to high dimensional problems than existing density estimation approaches.

Innovative And Additive Outlier Robust Kalman Filtering With A Robust Particle Filter

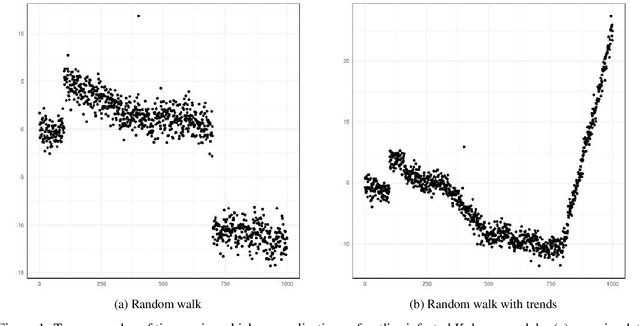
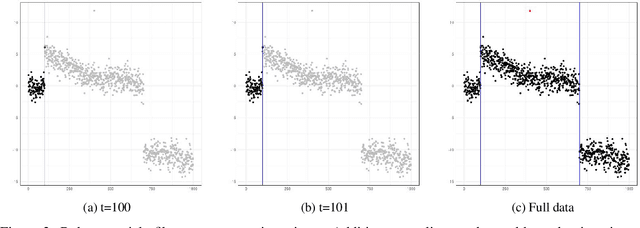
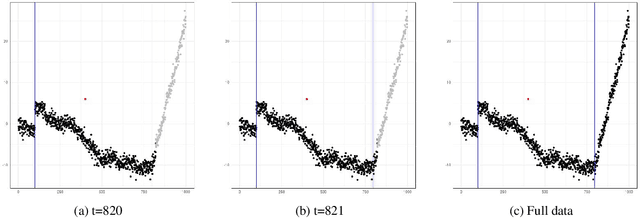
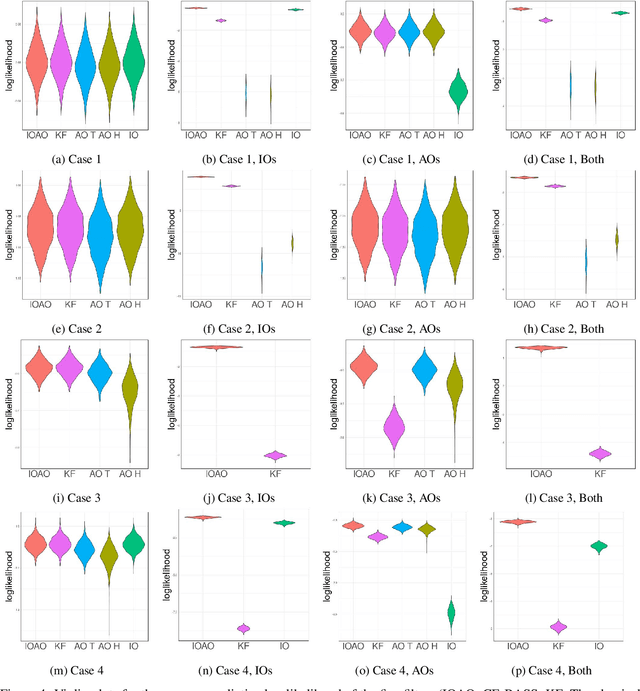
In this paper, we propose CE-BASS, a particle mixture Kalman filter which is robust to both innovative and additive outliers, and able to fully capture multi-modality in the distribution of the hidden state. Furthermore, the particle sampling approach re-samples past states, which enables CE-BASS to handle innovative outliers which are not immediately visible in the observations, such as trend changes. The filter is computationally efficient as we derive new, accurate approximations to the optimal proposal distributions for the particles. The proposed algorithm is shown to compare well with existing approaches and is applied to both machine temperature and server data.