Clustering Large Data Sets with Incremental Estimation of Low-density Separating Hyperplanes
Paper and Code
Aug 07, 2021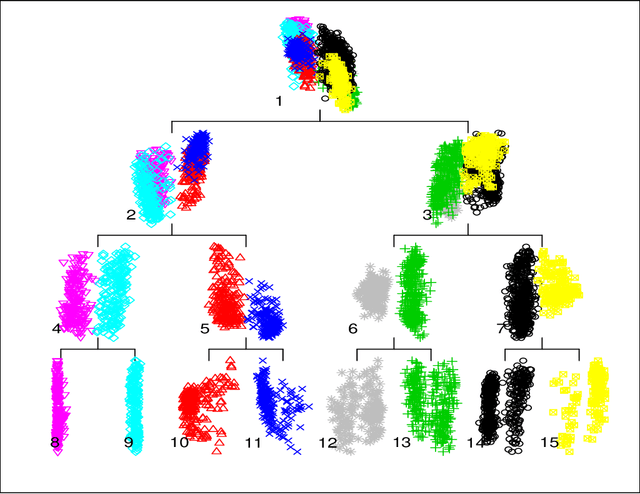
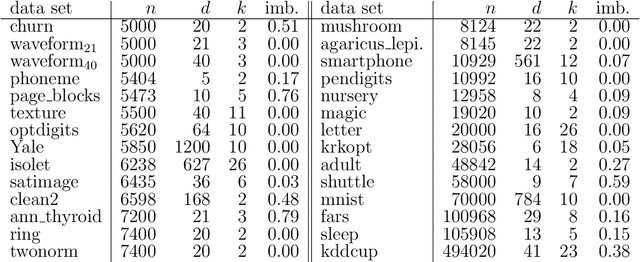
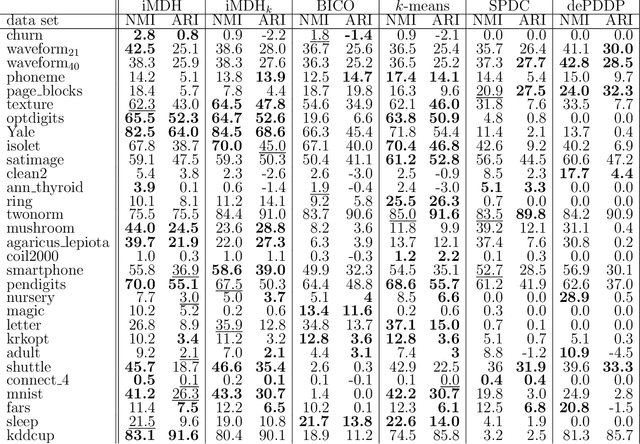
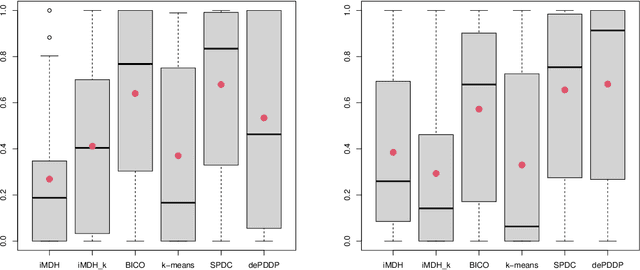
An efficient method for obtaining low-density hyperplane separators in the unsupervised context is proposed. Low density separators can be used to obtain a partition of a set of data based on their allocations to the different sides of the separators. The proposed method is based on applying stochastic gradient descent to the integrated density on the hyperplane with respect to a convolution of the underlying distribution and a smoothing kernel. In the case where the bandwidth of the smoothing kernel is decreased towards zero, the bias of these updates with respect to the true underlying density tends to zero, and convergence to a minimiser of the density on the hyperplane can be obtained. A post-processing of the partition induced by a collection of low-density hyperplanes yields an efficient and accurate clustering method which is capable of automatically selecting an appropriate number of clusters. Experiments with the proposed approach show that it is highly competitive in terms of both speed and accuracy when compared with relevant benchmarks. Code to implement the proposed approach is available in the form of an R package from https://github.com/DavidHofmeyr/iMDH.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge