Bayesian Optimization in a Billion Dimensions via Random Embeddings

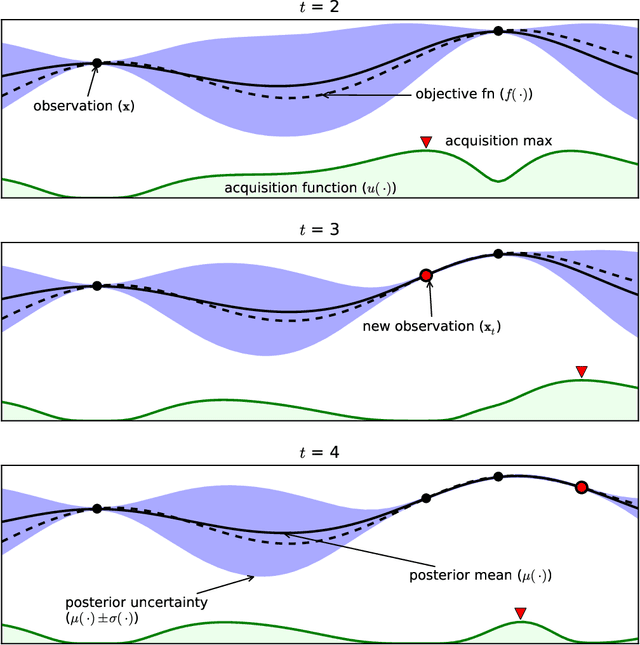
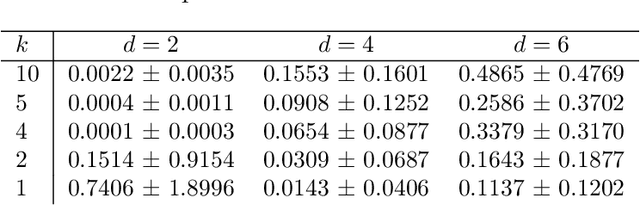
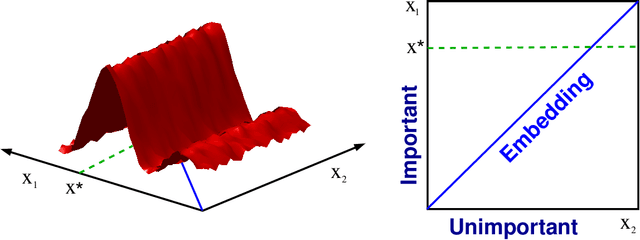
Bayesian optimization techniques have been successfully applied to robotics, planning, sensor placement, recommendation, advertising, intelligent user interfaces and automatic algorithm configuration. Despite these successes, the approach is restricted to problems of moderate dimension, and several workshops on Bayesian optimization have identified its scaling to high-dimensions as one of the holy grails of the field. In this paper, we introduce a novel random embedding idea to attack this problem. The resulting Random EMbedding Bayesian Optimization (REMBO) algorithm is very simple, has important invariance properties, and applies to domains with both categorical and continuous variables. We present a thorough theoretical analysis of REMBO. Empirical results confirm that REMBO can effectively solve problems with billions of dimensions, provided the intrinsic dimensionality is low. They also show that REMBO achieves state-of-the-art performance in optimizing the 47 discrete parameters of a popular mixed integer linear programming solver.

Narrowing the Gap: Random Forests In Theory and In Practice

Despite widespread interest and practical use, the theoretical properties of random forests are still not well understood. In this paper we contribute to this understanding in two ways. We present a new theoretically tractable variant of random regression forests and prove that our algorithm is consistent. We also provide an empirical evaluation, comparing our algorithm and other theoretically tractable random forest models to the random forest algorithm used in practice. Our experiments provide insight into the relative importance of different simplifications that theoreticians have made to obtain tractable models for analysis.

Consistency of Online Random Forests

As a testament to their success, the theory of random forests has long been outpaced by their application in practice. In this paper, we take a step towards narrowing this gap by providing a consistency result for online random forests.