Bayesian Optimization in a Billion Dimensions via Random Embeddings
Paper and Code
Jan 10, 2016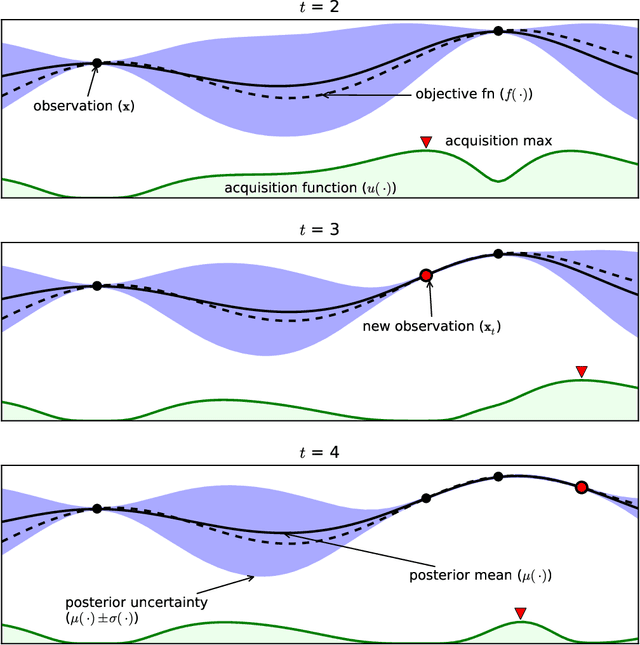
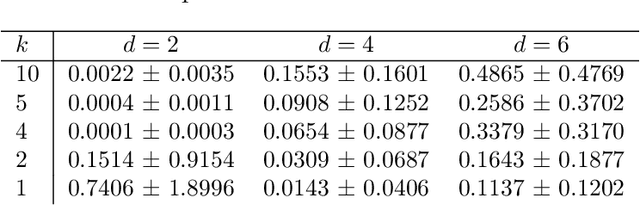
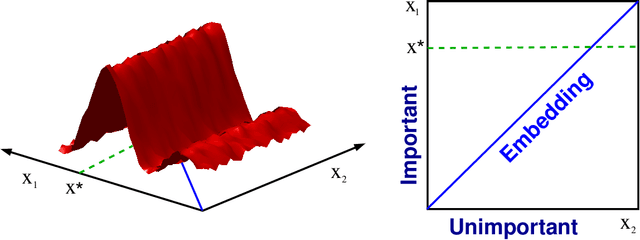

Bayesian optimization techniques have been successfully applied to robotics, planning, sensor placement, recommendation, advertising, intelligent user interfaces and automatic algorithm configuration. Despite these successes, the approach is restricted to problems of moderate dimension, and several workshops on Bayesian optimization have identified its scaling to high-dimensions as one of the holy grails of the field. In this paper, we introduce a novel random embedding idea to attack this problem. The resulting Random EMbedding Bayesian Optimization (REMBO) algorithm is very simple, has important invariance properties, and applies to domains with both categorical and continuous variables. We present a thorough theoretical analysis of REMBO. Empirical results confirm that REMBO can effectively solve problems with billions of dimensions, provided the intrinsic dimensionality is low. They also show that REMBO achieves state-of-the-art performance in optimizing the 47 discrete parameters of a popular mixed integer linear programming solver.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge