Denoising Multi-Source Weak Supervision for Neural Text Classification

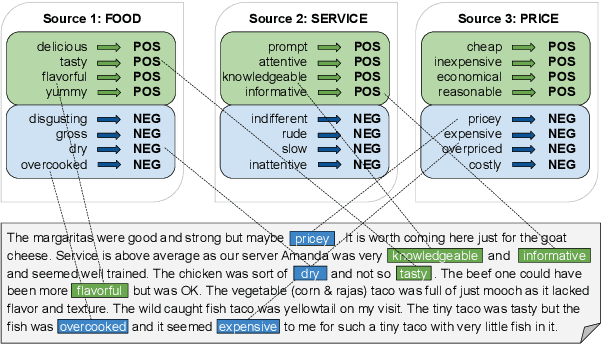
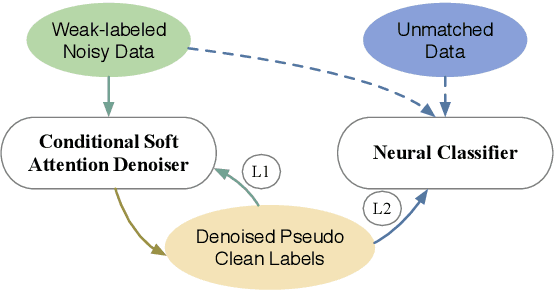
We study the problem of learning neural text classifiers without using any labeled data, but only easy-to-provide rules as multiple weak supervision sources. This problem is challenging because rule-induced weak labels are often noisy and incomplete. To address these two challenges, we design a label denoiser, which estimates the source reliability using a conditional soft attention mechanism and then reduces label noise by aggregating rule-annotated weak labels. The denoised pseudo labels then supervise a neural classifier to predicts soft labels for unmatched samples, which address the rule coverage issue. We evaluate our model on five benchmarks for sentiment, topic, and relation classifications. The results show that our model outperforms state-of-the-art weakly-supervised and semi-supervised methods consistently, and achieves comparable performance with fully-supervised methods even without any labeled data. Our code can be found at https://github.com/weakrules/Denoise-multi-weak-sources.

Forward Thinking: Building Deep Random Forests

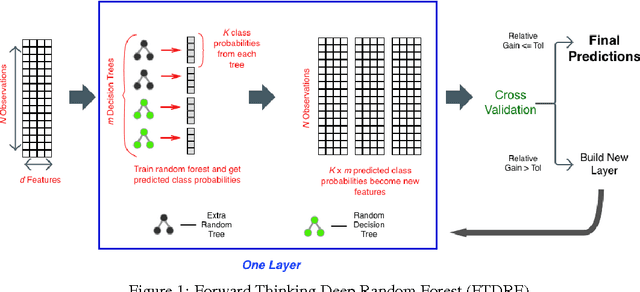
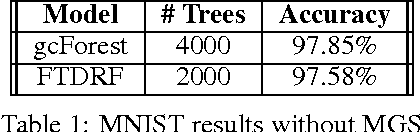
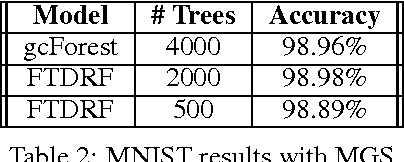
The success of deep neural networks has inspired many to wonder whether other learners could benefit from deep, layered architectures. We present a general framework called forward thinking for deep learning that generalizes the architectural flexibility and sophistication of deep neural networks while also allowing for (i) different types of learning functions in the network, other than neurons, and (ii) the ability to adaptively deepen the network as needed to improve results. This is done by training one layer at a time, and once a layer is trained, the input data are mapped forward through the layer to create a new learning problem. The process is then repeated, transforming the data through multiple layers, one at a time, rendering a new dataset, which is expected to be better behaved, and on which a final output layer can achieve good performance. In the case where the neurons of deep neural nets are replaced with decision trees, we call the result a Forward Thinking Deep Random Forest (FTDRF). We demonstrate a proof of concept by applying FTDRF on the MNIST dataset. We also provide a general mathematical formulation that allows for other types of deep learning problems to be considered.