Forward Thinking: Building and Training Neural Networks One Layer at a Time

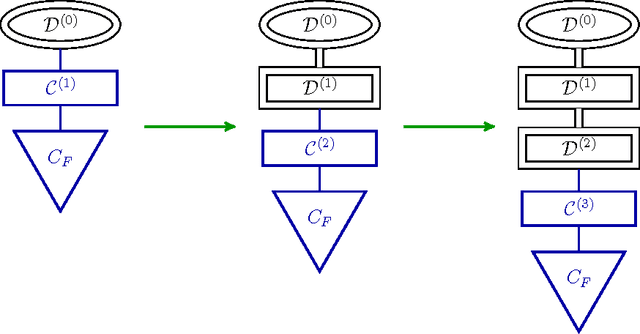
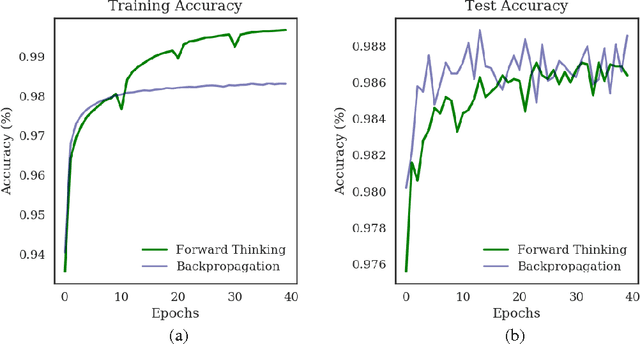
We present a general framework for training deep neural networks without backpropagation. This substantially decreases training time and also allows for construction of deep networks with many sorts of learners, including networks whose layers are defined by functions that are not easily differentiated, like decision trees. The main idea is that layers can be trained one at a time, and once they are trained, the input data are mapped forward through the layer to create a new learning problem. The process is repeated, transforming the data through multiple layers, one at a time, rendering a new data set, which is expected to be better behaved, and on which a final output layer can achieve good performance. We call this forward thinking and demonstrate a proof of concept by achieving state-of-the-art accuracy on the MNIST dataset for convolutional neural networks. We also provide a general mathematical formulation of forward thinking that allows for other types of deep learning problems to be considered.

Forward Thinking: Building Deep Random Forests

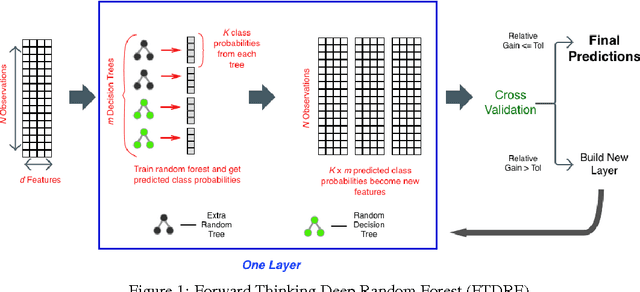
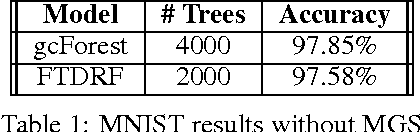
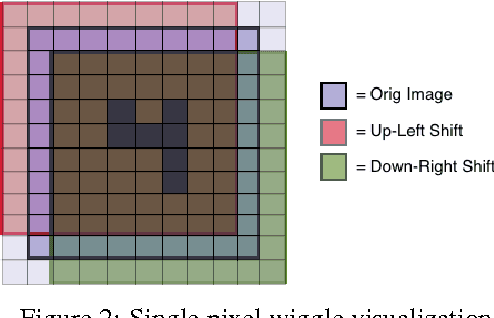
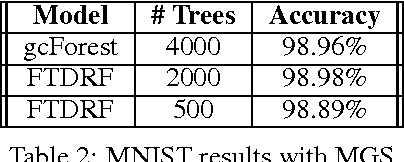
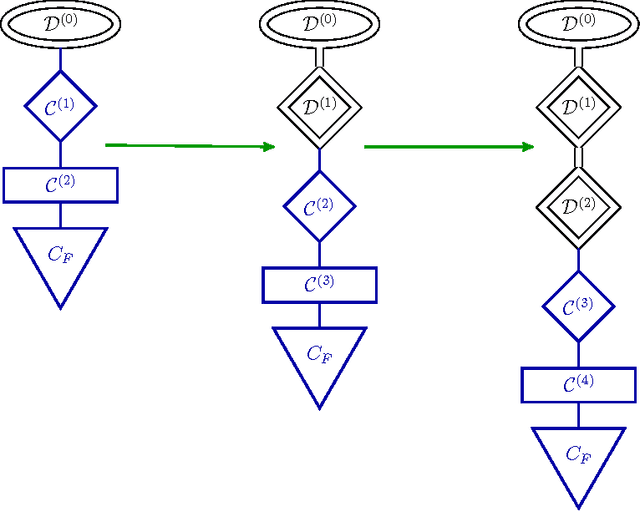
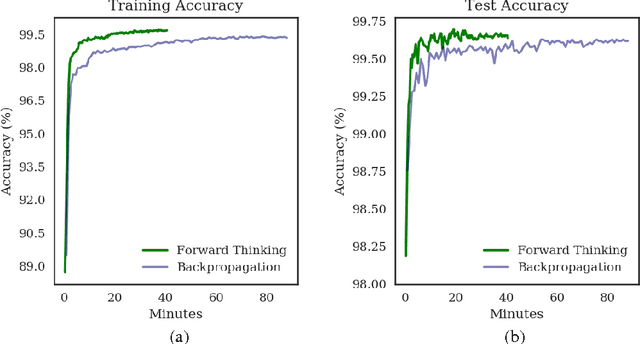
The success of deep neural networks has inspired many to wonder whether other learners could benefit from deep, layered architectures. We present a general framework called forward thinking for deep learning that generalizes the architectural flexibility and sophistication of deep neural networks while also allowing for (i) different types of learning functions in the network, other than neurons, and (ii) the ability to adaptively deepen the network as needed to improve results. This is done by training one layer at a time, and once a layer is trained, the input data are mapped forward through the layer to create a new learning problem. The process is then repeated, transforming the data through multiple layers, one at a time, rendering a new dataset, which is expected to be better behaved, and on which a final output layer can achieve good performance. In the case where the neurons of deep neural nets are replaced with decision trees, we call the result a Forward Thinking Deep Random Forest (FTDRF). We demonstrate a proof of concept by applying FTDRF on the MNIST dataset. We also provide a general mathematical formulation that allows for other types of deep learning problems to be considered.