Tandem Blocks in Deep Convolutional Neural Networks

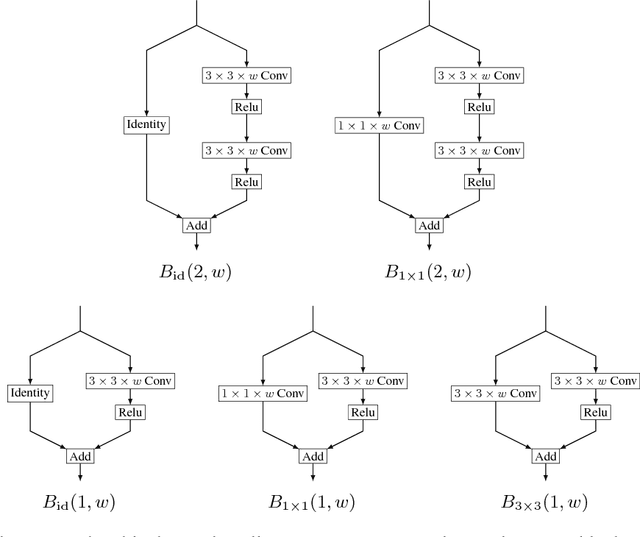
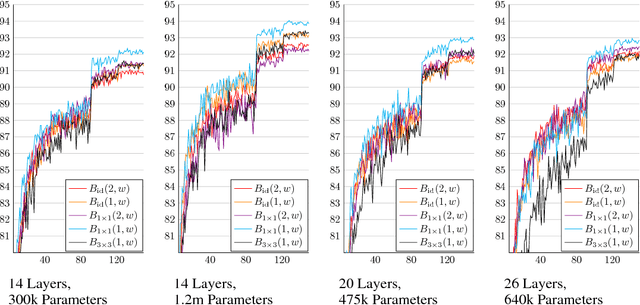
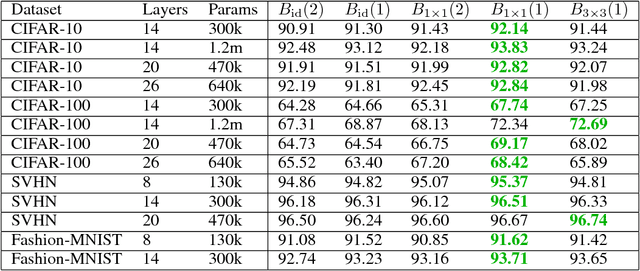
Due to the success of residual networks (resnets) and related architectures, shortcut connections have quickly become standard tools for building convolutional neural networks. The explanations in the literature for the apparent effectiveness of shortcuts are varied and often contradictory. We hypothesize that shortcuts work primarily because they act as linear counterparts to nonlinear layers. We test this hypothesis by using several variations on the standard residual block, with different types of linear connections, to build small image classification networks. Our experiments show that other kinds of linear connections can be even more effective than the identity shortcuts. Our results also suggest that the best type of linear connection for a given application may depend on both network width and depth.

Forward Thinking: Building and Training Neural Networks One Layer at a Time

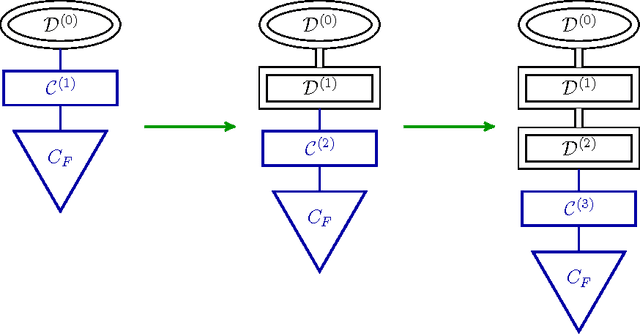
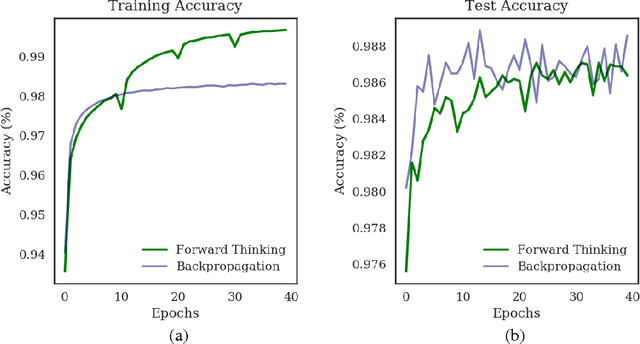
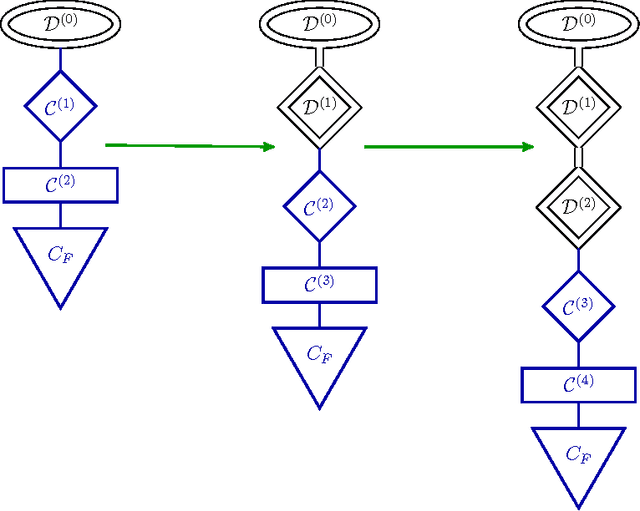
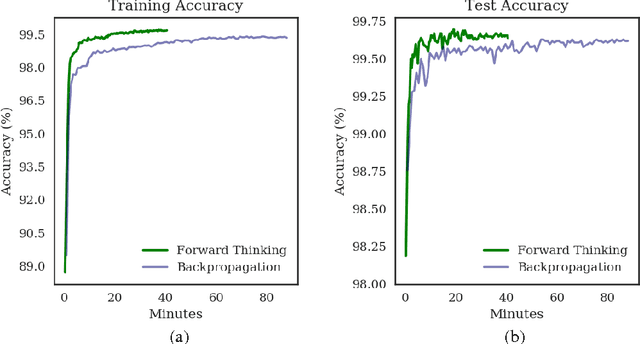
We present a general framework for training deep neural networks without backpropagation. This substantially decreases training time and also allows for construction of deep networks with many sorts of learners, including networks whose layers are defined by functions that are not easily differentiated, like decision trees. The main idea is that layers can be trained one at a time, and once they are trained, the input data are mapped forward through the layer to create a new learning problem. The process is repeated, transforming the data through multiple layers, one at a time, rendering a new data set, which is expected to be better behaved, and on which a final output layer can achieve good performance. We call this forward thinking and demonstrate a proof of concept by achieving state-of-the-art accuracy on the MNIST dataset for convolutional neural networks. We also provide a general mathematical formulation of forward thinking that allows for other types of deep learning problems to be considered.