Fractional order magnetic resonance fingerprinting in the human cerebral cortex

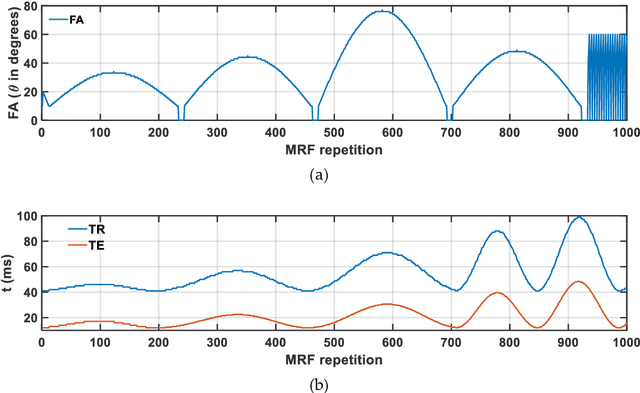
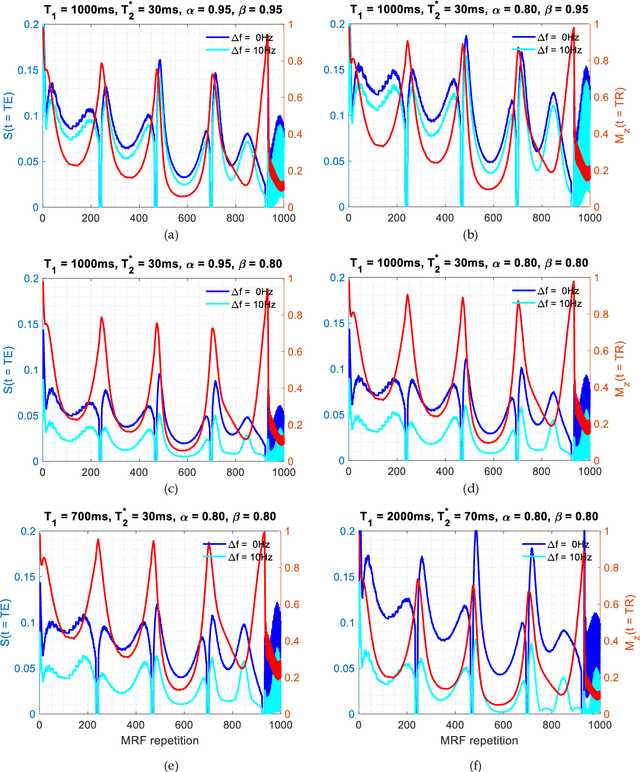
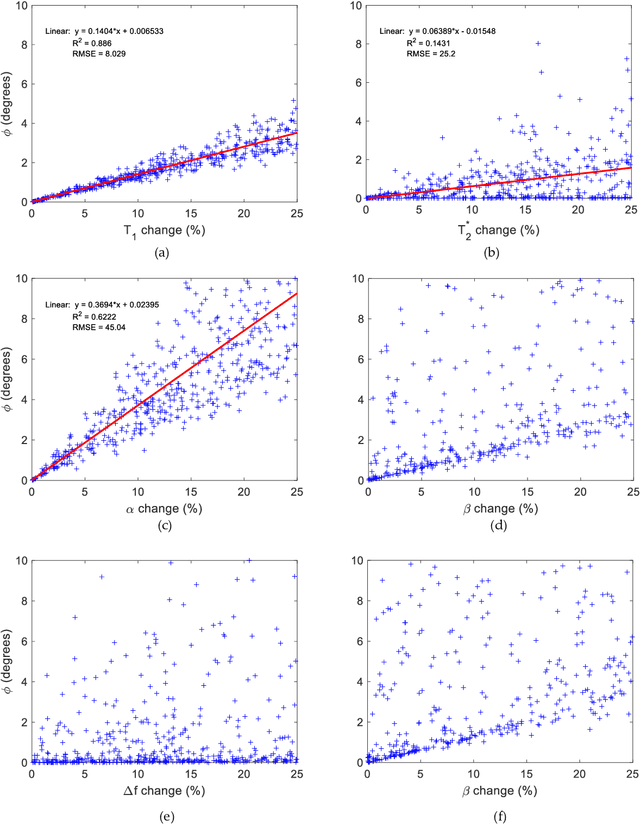
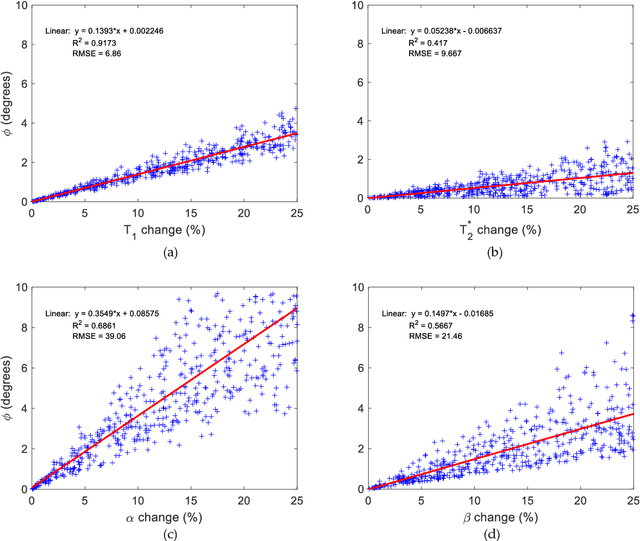
Mathematical models are becoming increasingly important in magnetic resonance imaging (MRI), as they provide a mechanistic approach for making a link between tissue microstructure and signals acquired using the medical imaging instrument. The Bloch equations, which describes spin and relaxation in a magnetic field, is a set of integer order differential equations with a solution exhibiting mono-exponential behaviour in time. Parameters of the model may be estimated using a non-linear solver, or by creating a dictionary of model parameters from which MRI signals are simulated and then matched with experiment. We have previously shown the potential efficacy of a magnetic resonance fingerprinting (MRF) approach, i.e. dictionary matching based on the classical Bloch equations, for parcellating the human cerebral cortex. However, this classical model is unable to describe in full the mm-scale MRI signal generated based on an heterogenous and complex tissue micro-environment. The time-fractional order Bloch equations has been shown to provide, as a function of time, a good fit of brain MRI signals. We replaced the integer order Bloch equations with the previously reported time-fractional counterpart within the MRF framework and performed experiments to parcellate human gray matter, which is cortical brain tissue with different cyto-architecture at different spatial locations. Our findings suggest that the time-fractional order parameters, {\alpha} and {\beta}, potentially associate with the effect of interareal architectonic variability, hypothetically leading to more accurate cortical parcellation.

CNNs and GANs in MRI-based cross-modality medical image estimation

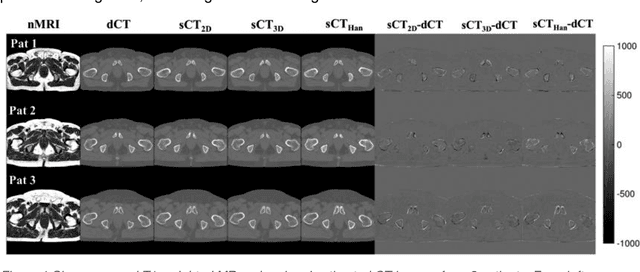
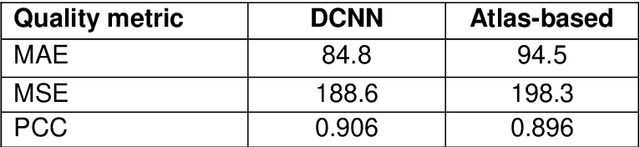
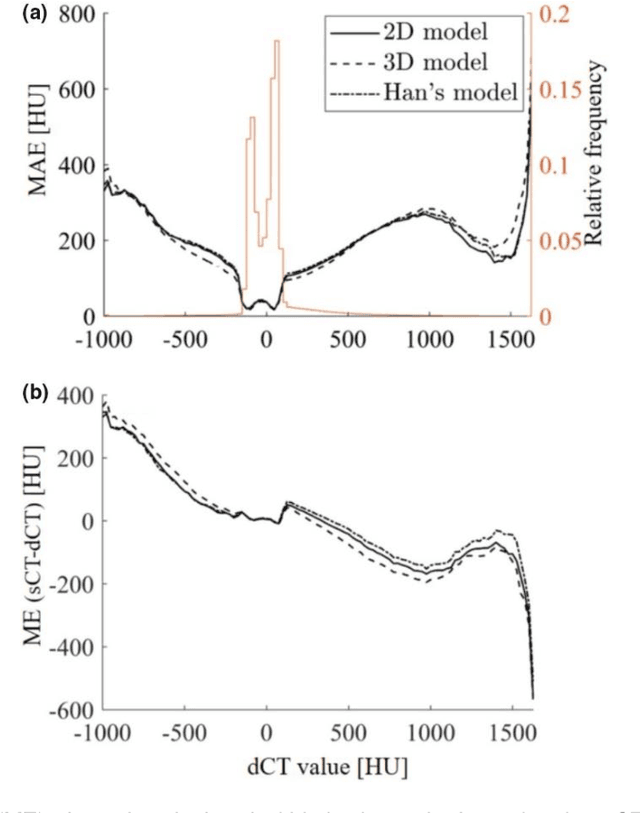
Cross-modality image estimation involves the generation of images of one medical imaging modality from that of another modality. Convolutional neural networks (CNNs) have been shown to be useful in identifying, characterising and extracting image patterns. Generative adversarial networks (GANs) use CNNs as generators and estimated images are discriminated as true or false based on an additional network. CNNs and GANs within the image estimation framework may be considered more generally as deep learning approaches, since imaging data tends to be large, leading to a larger number of network weights. Almost all research in the CNN/GAN image estimation literature has involved the use of MRI data with the other modality primarily being PET or CT. This review provides an overview of the use of CNNs and GANs for MRI-based cross-modality medical image estimation. We outline the neural networks implemented, and detail network constructs employed for CNN and GAN image-to-image estimators. Motivations behind cross-modality image estimation are provided as well. GANs appear to provide better utility in cross-modality image estimation in comparison with CNNs, a finding drawn based on our analysis involving metrics comparing estimated and actual images. Our final remarks highlight key challenges faced by the cross-modality medical image estimation field, and suggestions for future research are outlined.

Optimal-margin evolutionary classifier

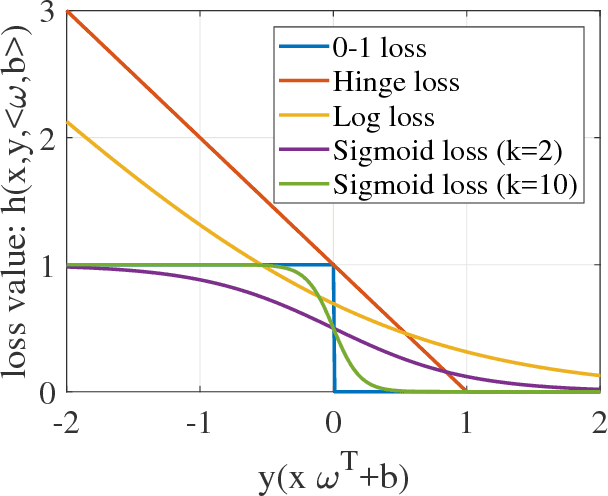
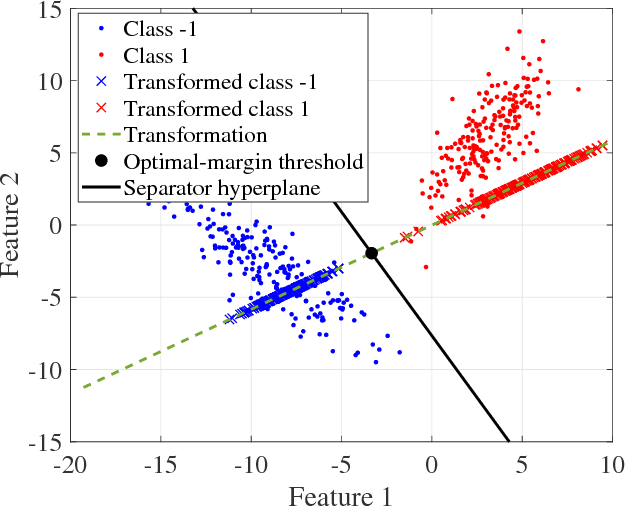
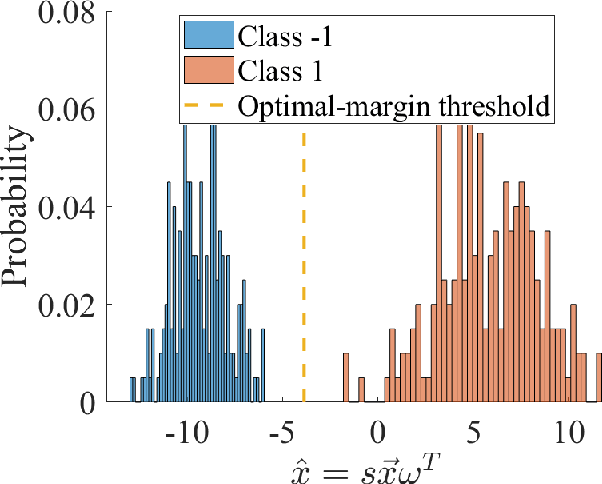
We introduce a novel approach for discriminative classification using evolutionary algorithms. We first propose an algorithm to optimize the total loss value using a modified 0-1 loss function in a one-dimensional space for classification. We then extend this algorithm for multi-dimensional classification using an evolutionary algorithm. The proposed evolutionary algorithm aims to find a hyperplane which best classifies instances while minimizes the classification risk. We test particle swarm optimization, evolutionary strategy, and covariance matrix adaptation evolutionary strategy for optimization purpose. Finally, we compare our results with well-established and state-of-the-art classification algorithms, for both binary and multi-class classification, on 19 benchmark classification problems, with and without noise and outliers. Results show that the performance of the proposed algorithm is significantly (t-test) better than all other methods in almost all problems tested. We also show that the proposed algorithm is significantly more robust against noise and outliers comparing to other methods. The running time of the algorithm is within a reasonable range for the solution of real-world classification problems.

Linear centralization classifier

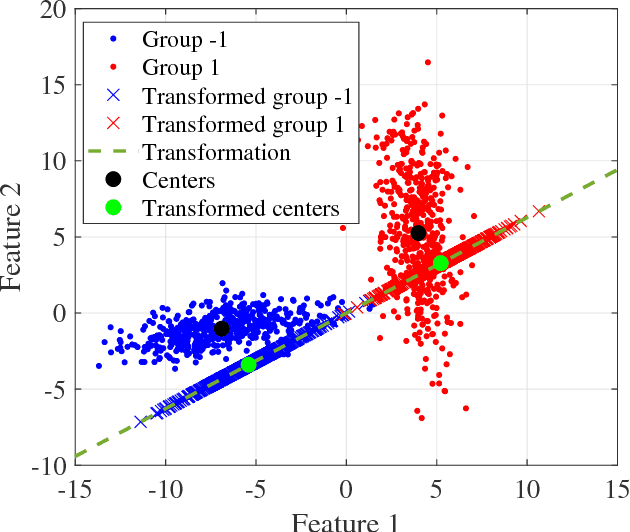
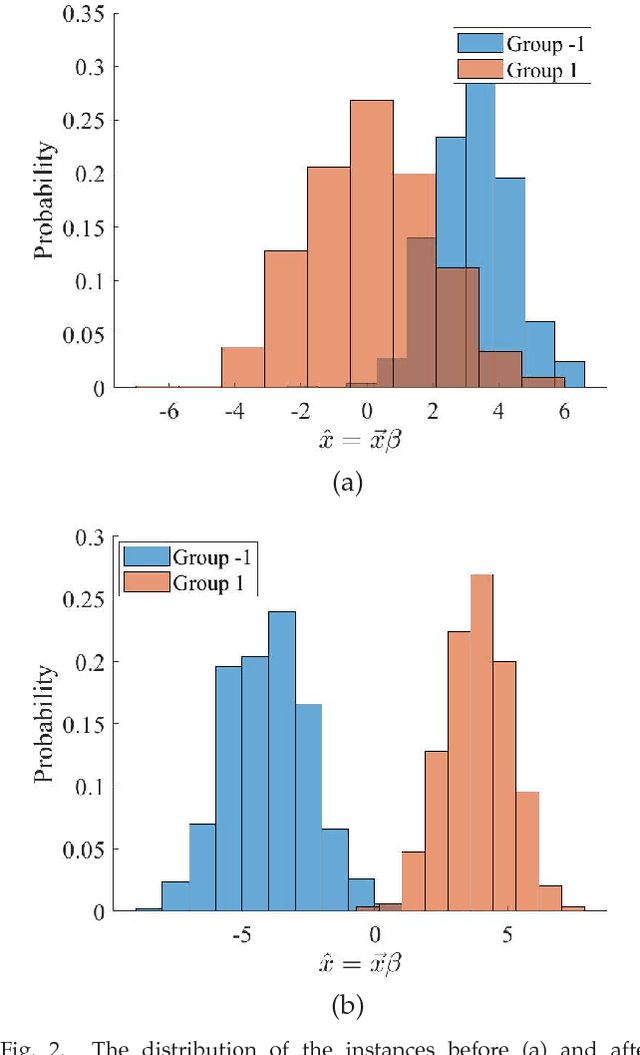
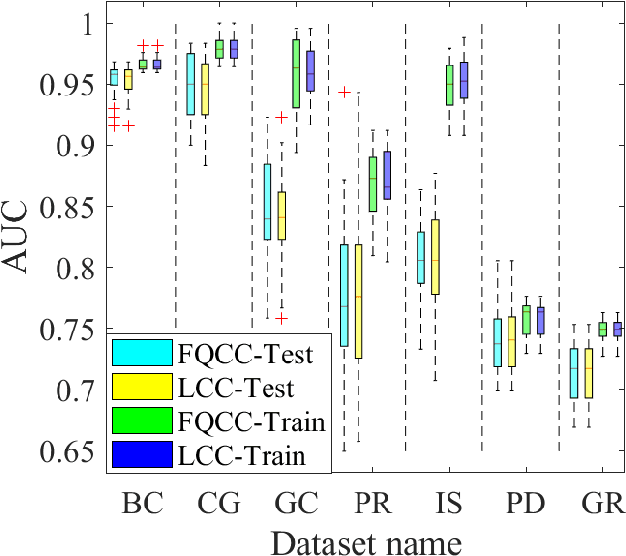
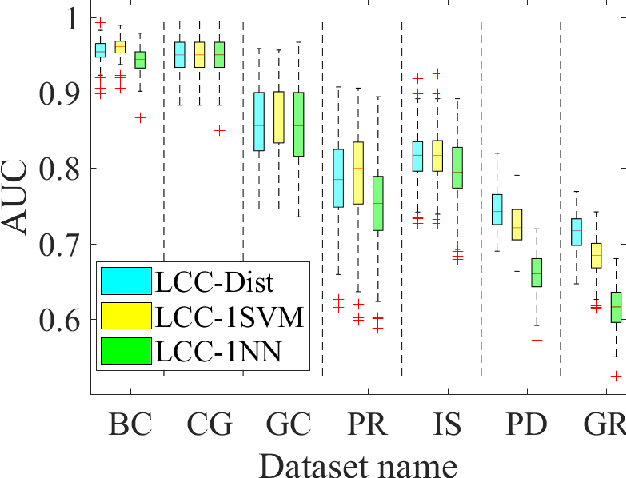
A classification algorithm, called the Linear Centralization Classifier (LCC), is introduced. The algorithm seeks to find a transformation that best maps instances from the feature space to a space where they concentrate towards the center of their own classes, while maximimizing the distance between class centers. We formulate the classifier as a quadratic program with quadratic constraints. We then simplify this formulation to a linear program that can be solved effectively using a linear programming solver (e.g., simplex-dual). We extend the formulation for LCC to enable the use of kernel functions for non-linear classification applications. We compare our method with two standard classification methods (support vector machine and linear discriminant analysis) and four state-of-the-art classification methods when they are applied to eight standard classification datasets. Our experimental results show that LCC is able to classify instances more accurately (based on the area under the receiver operating characteristic) in comparison to other tested methods on the chosen datasets. We also report the results for LCC with a particular kernel to solve for synthetic non-linear classification problems.

Optimization of distributions differences for classification

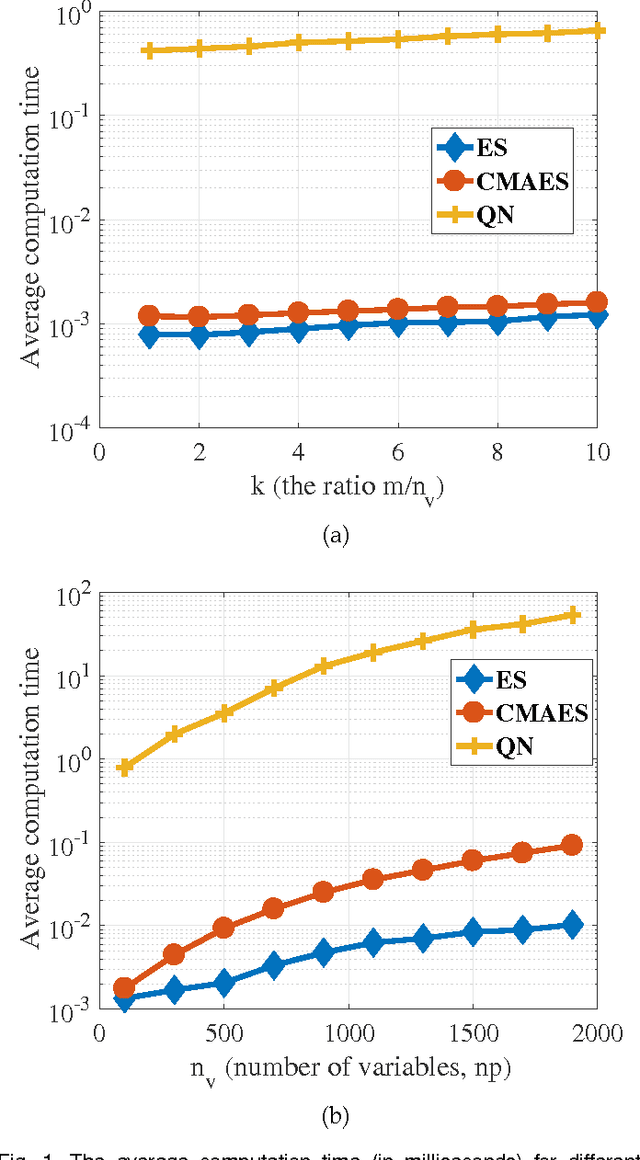
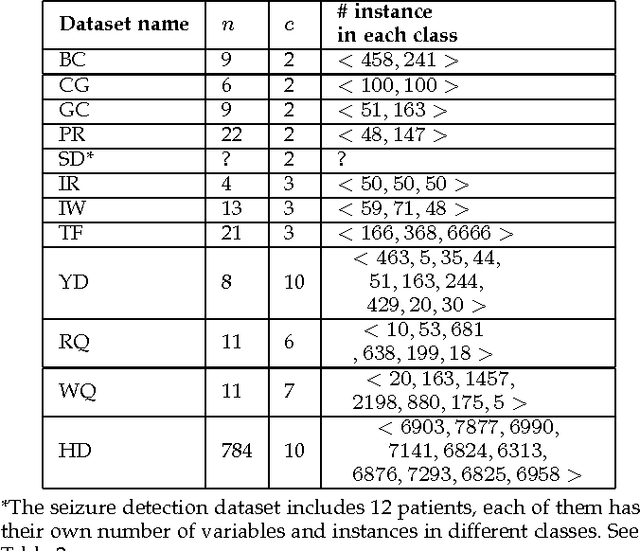
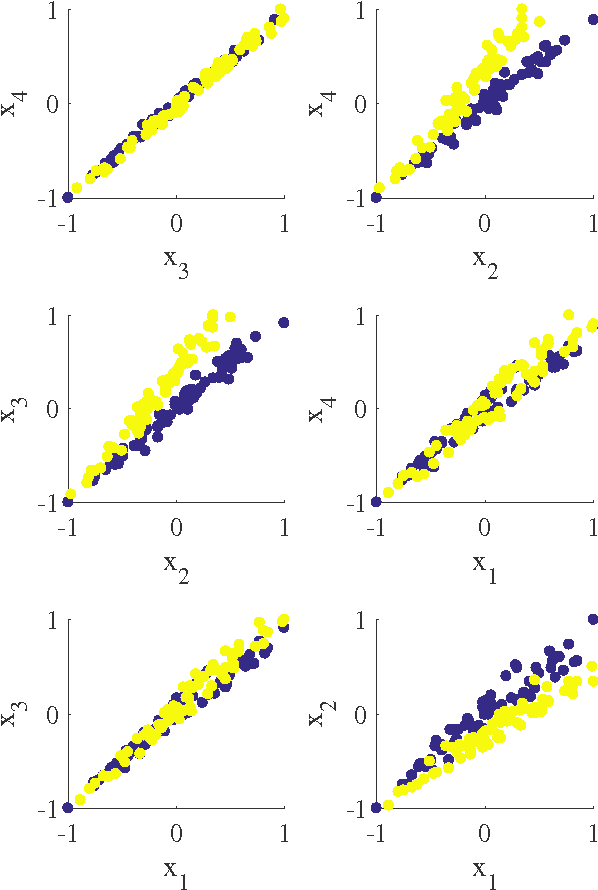
In this paper we introduce a new classification algorithm called Optimization of Distributions Differences (ODD). The algorithm aims to find a transformation from the feature space to a new space where the instances in the same class are as close as possible to one another while the gravity centers of these classes are as far as possible from one another. This aim is formulated as a multiobjective optimization problem that is solved by a hybrid of an evolutionary strategy and the Quasi-Newton method. The choice of the transformation function is flexible and could be any continuous space function. We experiment with a linear and a non-linear transformation in this paper. We show that the algorithm can outperform 6 other state-of-the-art classification methods, namely naive Bayes, support vector machines, linear discriminant analysis, multi-layer perceptrons, decision trees, and k-nearest neighbors, in 12 standard classification datasets. Our results show that the method is less sensitive to the imbalanced number of instances comparing to these methods. We also show that ODD maintains its performance better than other classification methods in these datasets, hence, offers a better generalization ability.