Linear centralization classifier
Paper and Code
Dec 22, 2017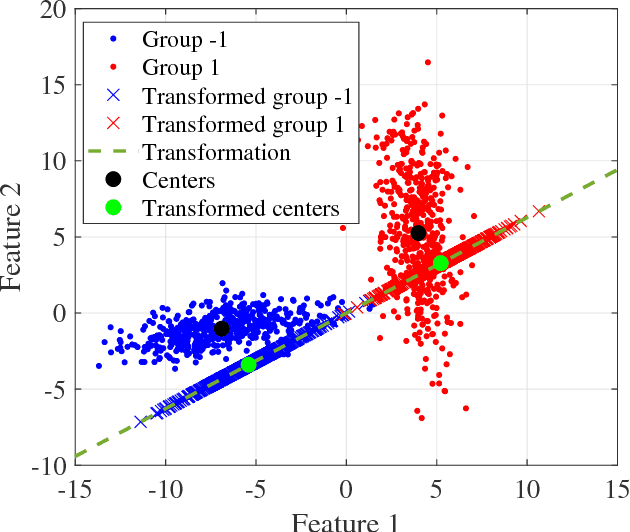
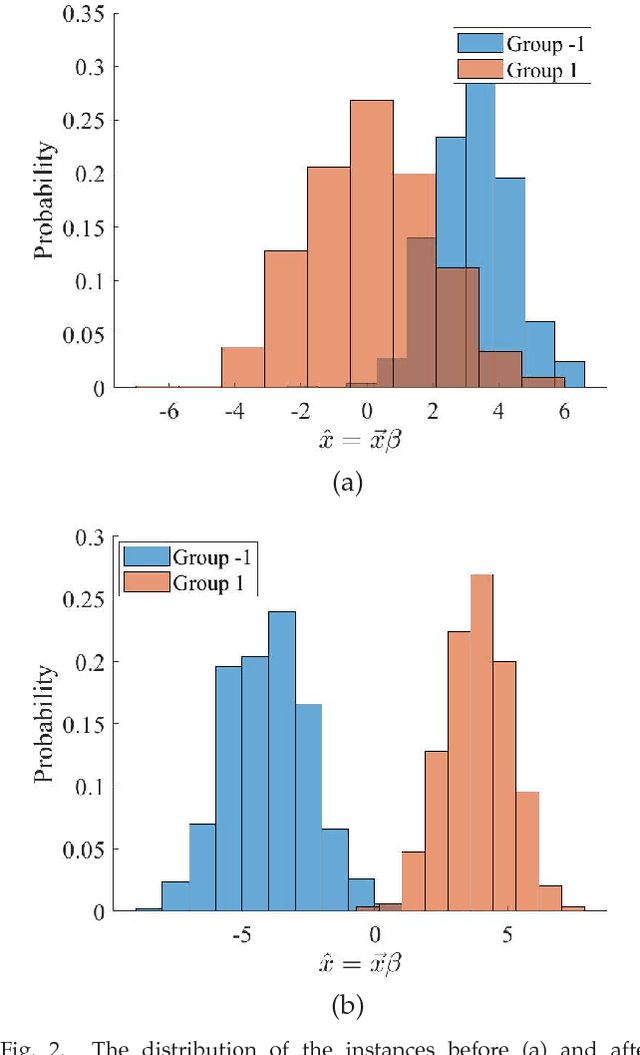
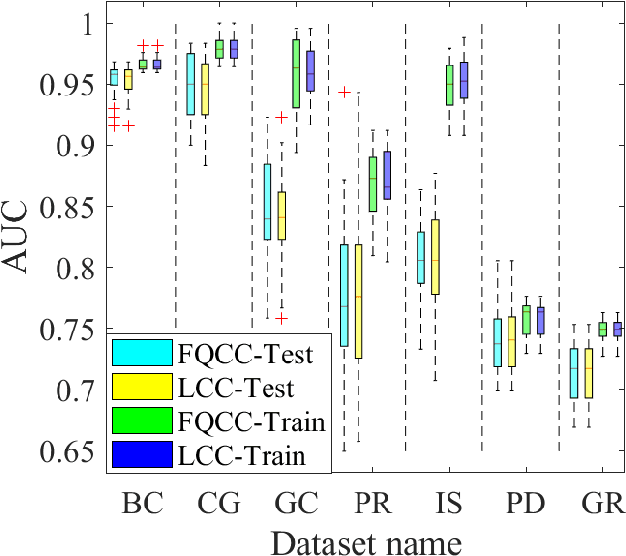
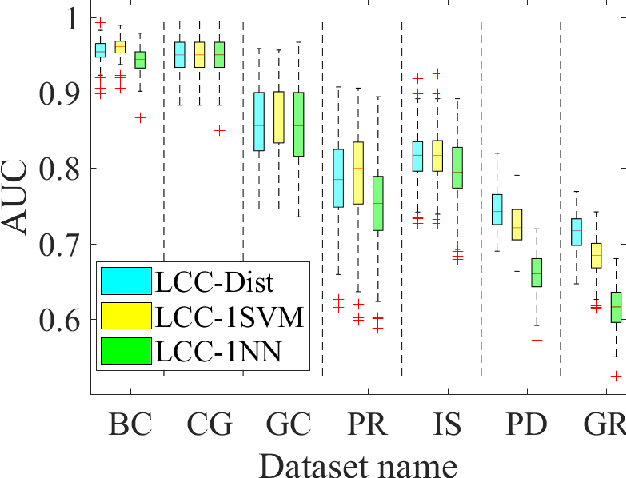
A classification algorithm, called the Linear Centralization Classifier (LCC), is introduced. The algorithm seeks to find a transformation that best maps instances from the feature space to a space where they concentrate towards the center of their own classes, while maximimizing the distance between class centers. We formulate the classifier as a quadratic program with quadratic constraints. We then simplify this formulation to a linear program that can be solved effectively using a linear programming solver (e.g., simplex-dual). We extend the formulation for LCC to enable the use of kernel functions for non-linear classification applications. We compare our method with two standard classification methods (support vector machine and linear discriminant analysis) and four state-of-the-art classification methods when they are applied to eight standard classification datasets. Our experimental results show that LCC is able to classify instances more accurately (based on the area under the receiver operating characteristic) in comparison to other tested methods on the chosen datasets. We also report the results for LCC with a particular kernel to solve for synthetic non-linear classification problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge