Quang M. Tieng
Optimization of distributions differences for classification
Mar 02, 2017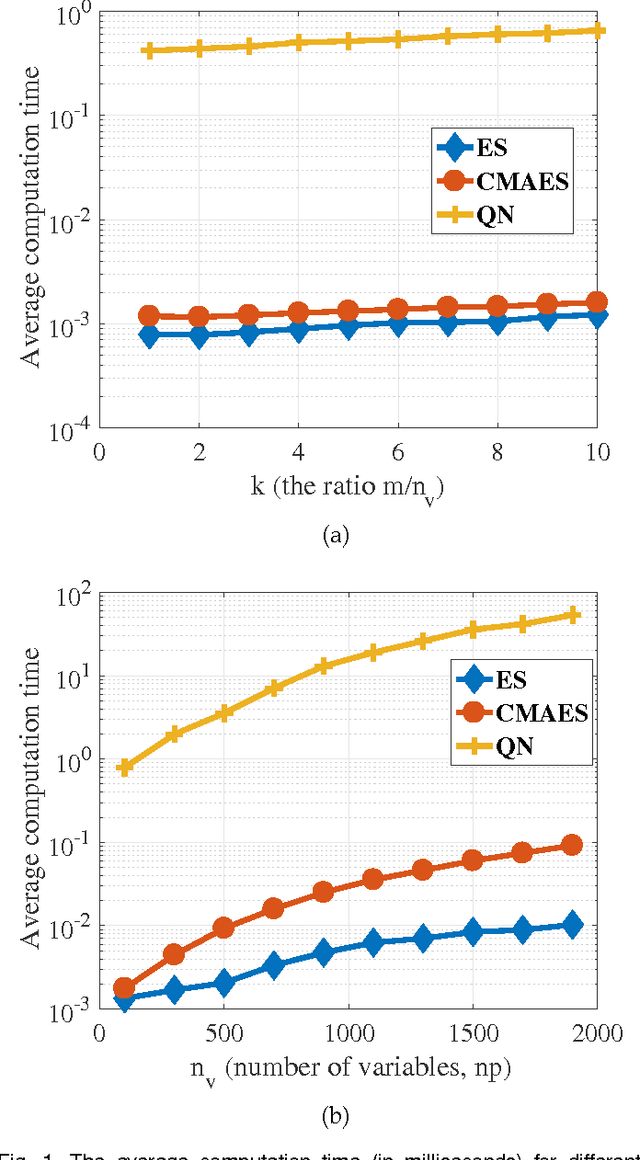
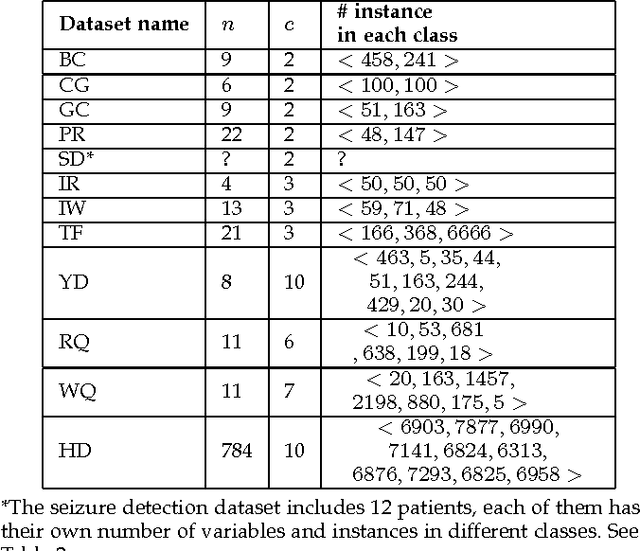
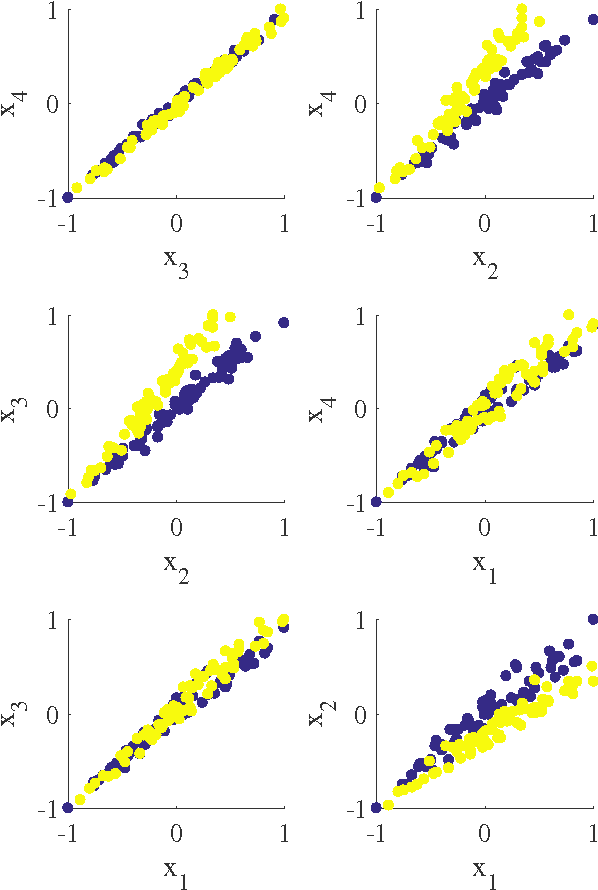
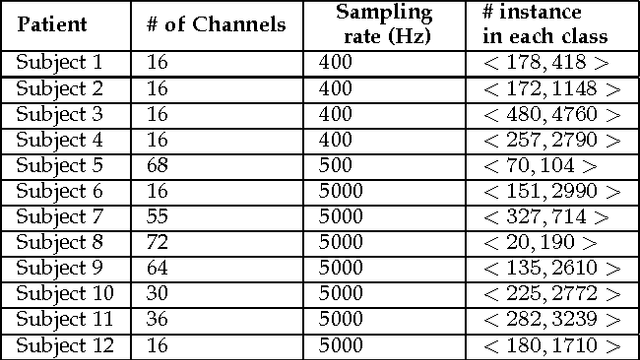
Abstract:In this paper we introduce a new classification algorithm called Optimization of Distributions Differences (ODD). The algorithm aims to find a transformation from the feature space to a new space where the instances in the same class are as close as possible to one another while the gravity centers of these classes are as far as possible from one another. This aim is formulated as a multiobjective optimization problem that is solved by a hybrid of an evolutionary strategy and the Quasi-Newton method. The choice of the transformation function is flexible and could be any continuous space function. We experiment with a linear and a non-linear transformation in this paper. We show that the algorithm can outperform 6 other state-of-the-art classification methods, namely naive Bayes, support vector machines, linear discriminant analysis, multi-layer perceptrons, decision trees, and k-nearest neighbors, in 12 standard classification datasets. Our results show that the method is less sensitive to the imbalanced number of instances comparing to these methods. We also show that ODD maintains its performance better than other classification methods in these datasets, hence, offers a better generalization ability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge