Fractional order magnetic resonance fingerprinting in the human cerebral cortex
Paper and Code
Jun 09, 2021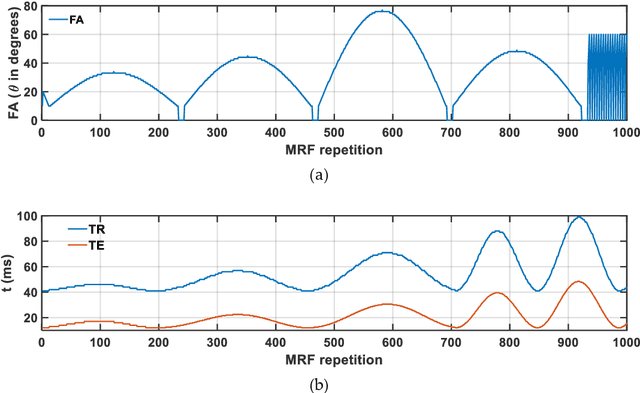
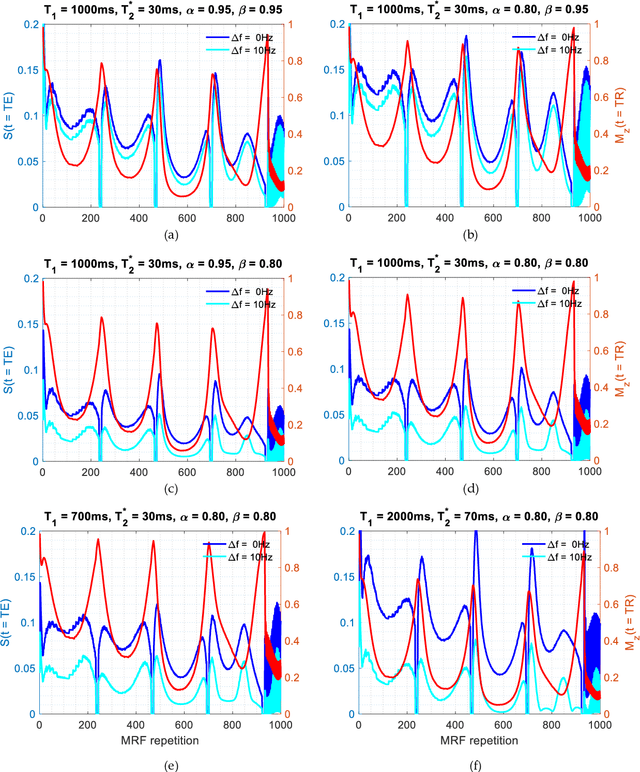
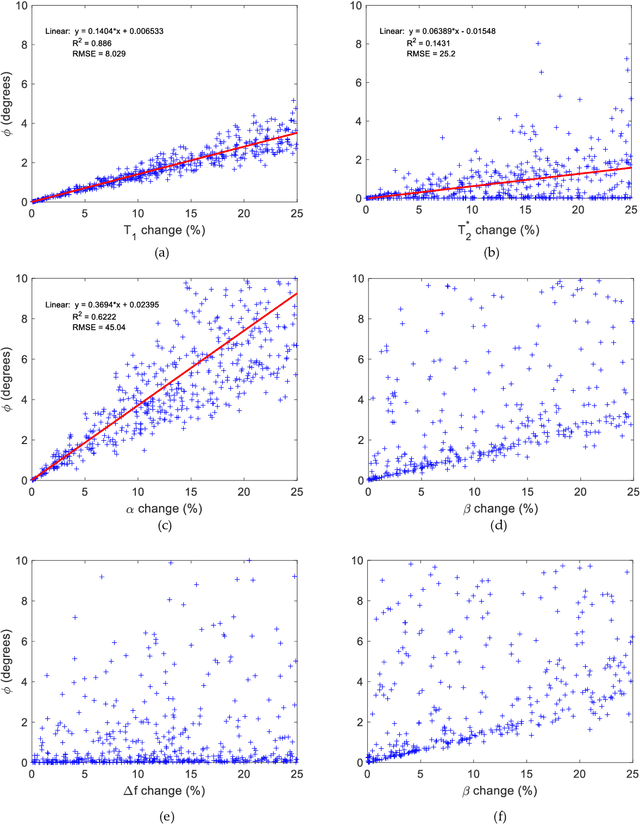
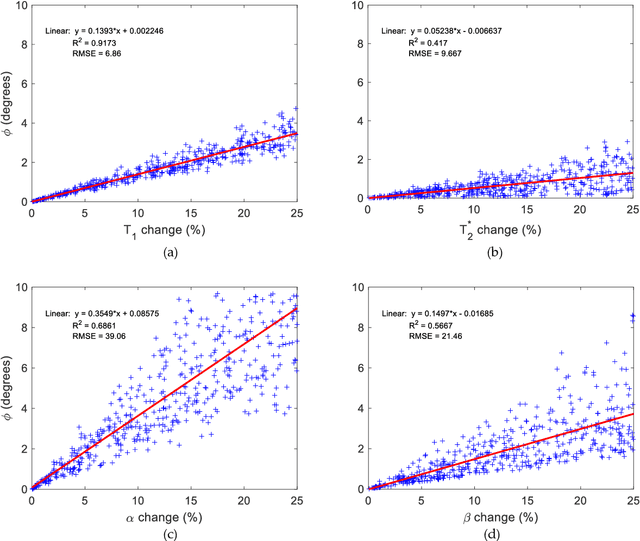
Mathematical models are becoming increasingly important in magnetic resonance imaging (MRI), as they provide a mechanistic approach for making a link between tissue microstructure and signals acquired using the medical imaging instrument. The Bloch equations, which describes spin and relaxation in a magnetic field, is a set of integer order differential equations with a solution exhibiting mono-exponential behaviour in time. Parameters of the model may be estimated using a non-linear solver, or by creating a dictionary of model parameters from which MRI signals are simulated and then matched with experiment. We have previously shown the potential efficacy of a magnetic resonance fingerprinting (MRF) approach, i.e. dictionary matching based on the classical Bloch equations, for parcellating the human cerebral cortex. However, this classical model is unable to describe in full the mm-scale MRI signal generated based on an heterogenous and complex tissue micro-environment. The time-fractional order Bloch equations has been shown to provide, as a function of time, a good fit of brain MRI signals. We replaced the integer order Bloch equations with the previously reported time-fractional counterpart within the MRF framework and performed experiments to parcellate human gray matter, which is cortical brain tissue with different cyto-architecture at different spatial locations. Our findings suggest that the time-fractional order parameters, {\alpha} and {\beta}, potentially associate with the effect of interareal architectonic variability, hypothetically leading to more accurate cortical parcellation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge