Bayesian Graph Traversal

This research considers Bayesian decision-analytic approaches toward the traversal of an uncertain graph. Namely, a traveler progresses over a graph in which rewards are gained upon a node's first visit and costs are incurred for every edge traversal. The traveler knows the graph's adjacency matrix and his starting position but does not know the rewards and costs. The traveler is a Bayesian who encodes his beliefs about these values using a Gaussian process prior and who seeks to maximize his expected utility over these beliefs. Adopting a decision-analytic perspective, we develop sequential decision-making solution strategies for this coupled information-collection and network-routing problem. We show that the problem is NP-Hard and derive properties of the optimal walk. These properties provide heuristics for the traveler's problem that balance exploration and exploitation. We provide a practical case study focused on the use of unmanned aerial systems for public safety and empirically study policy performance in myriad Erdos-Renyi settings.

A Statistician Teaches Deep Learning

Deep learning (DL) has gained much attention and become increasingly popular in modern data science. Computer scientists led the way in developing deep learning techniques, so the ideas and perspectives can seem alien to statisticians. Nonetheless, it is important that statisticians become involved -- many of our students need this expertise for their careers. In this paper, developed as part of a program on DL held at the Statistical and Applied Mathematical Sciences Institute, we address this culture gap and provide tips on how to teach deep learning to statistics graduate students. After some background, we list ways in which DL and statistical perspectives differ, provide a recommended syllabus that evolved from teaching two iterations of a DL graduate course, offer examples of suggested homework assignments, give an annotated list of teaching resources, and discuss DL in the context of two research areas.

Modeling community structure and topics in dynamic text networks

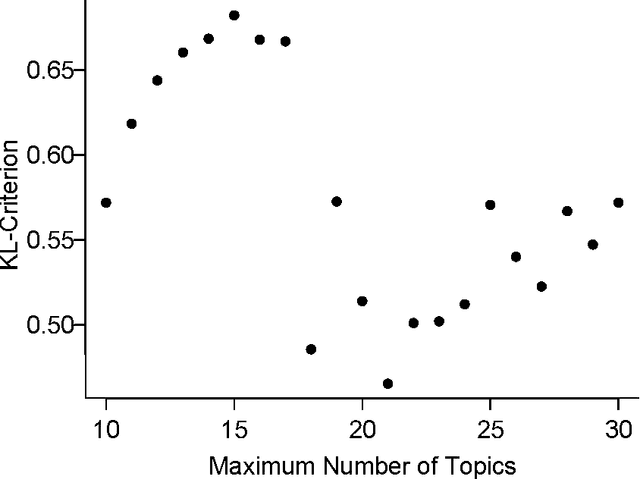
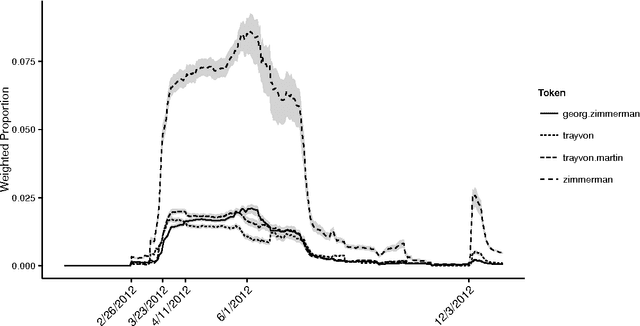
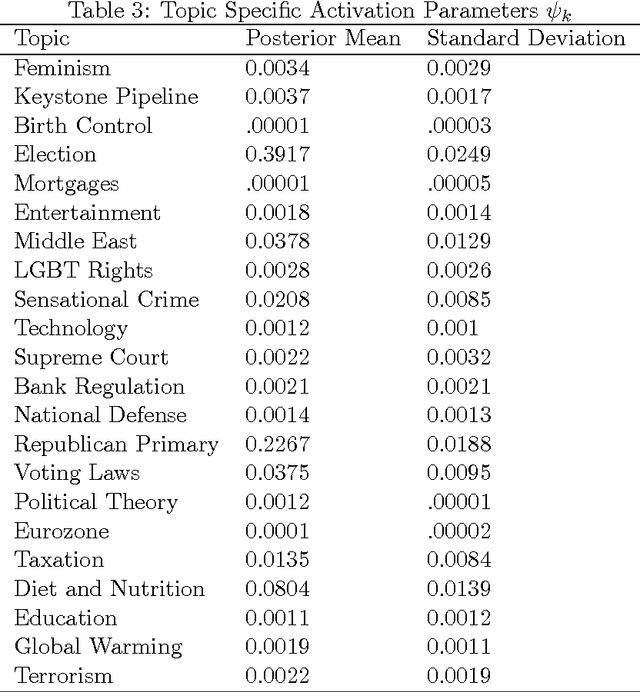
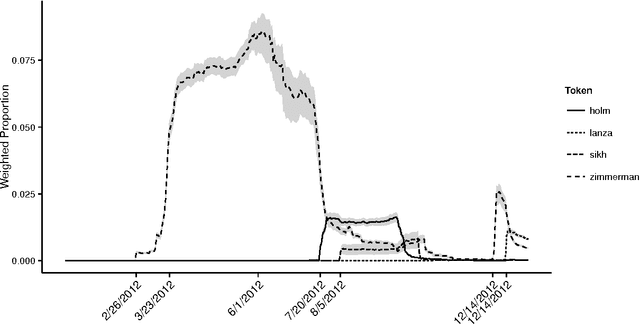
The last decade has seen great progress in both dynamic network modeling and topic modeling. This paper draws upon both areas to create a Bayesian method that allows topic discovery to inform the latent network model and the network structure to facilitate topic identification. We apply this method to the 467 top political blogs of 2012. Our results find complex community structure within this set of blogs, where community membership depends strongly upon the set of topics in which the blogger is interested.

Directional Mean Curvature for Textured Image Demixing

Approximation theory plays an important role in image processing, especially image deconvolution and decomposition. For piecewise smooth images, there are many methods that have been developed over the past thirty years. The goal of this study is to devise similar and practical methodology for handling textured images. This problem is motivated by forensic imaging, since fingerprints, shoeprints and bullet ballistic evidence are textured images. In particular, it is known that texture information is almost destroyed by a blur operator, such as a blurred ballistic image captured from a low-cost microscope. The contribution of this work is twofold: first, we propose a mathematical model for textured image deconvolution and decomposition into four meaningful components, using a high-order partial differential equation approach based on the directional mean curvature. Second, we uncover a link between functional analysis and multiscale sampling theory, e.g., harmonic analysis and filter banks. Both theoretical results and examples with natural images are provided to illustrate the performance of the proposed model.