A purely data-driven framework for prediction, optimization, and control of networked processes: application to networked SIS epidemic model

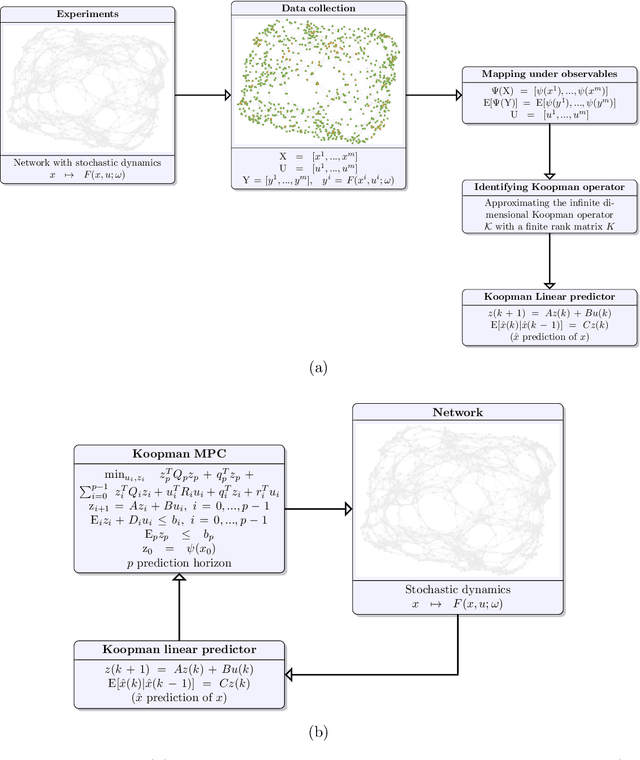
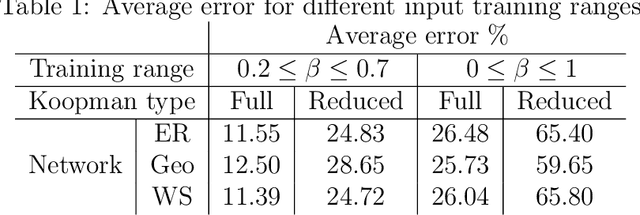
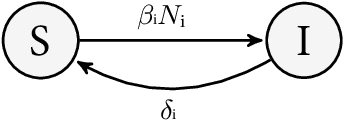
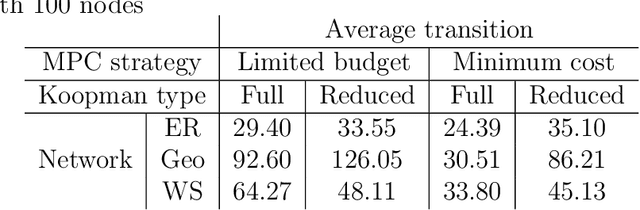
Networks are landmarks of many complex phenomena where interweaving interactions between different agents transform simple local rule-sets into nonlinear emergent behaviors. While some recent studies unveil associations between the network structure and the underlying dynamical process, identifying stochastic nonlinear dynamical processes continues to be an outstanding problem. Here we develop a simple data-driven framework based on operator-theoretic techniques to identify and control stochastic nonlinear dynamics taking place over large-scale networks. The proposed approach requires no prior knowledge of the network structure and identifies the underlying dynamics solely using a collection of two-step snapshots of the states. This data-driven system identification is achieved by using the Koopman operator to find a low dimensional representation of the dynamical patterns that evolve linearly. Further, we use the global linear Koopman model to solve critical control problems by applying to model predictive control (MPC)--typically, a challenging proposition when applied to large networks. We show that our proposed approach tackles this by converting the original nonlinear programming into a more tractable optimization problem that is both convex and with far fewer variables.

Modeling community structure and topics in dynamic text networks

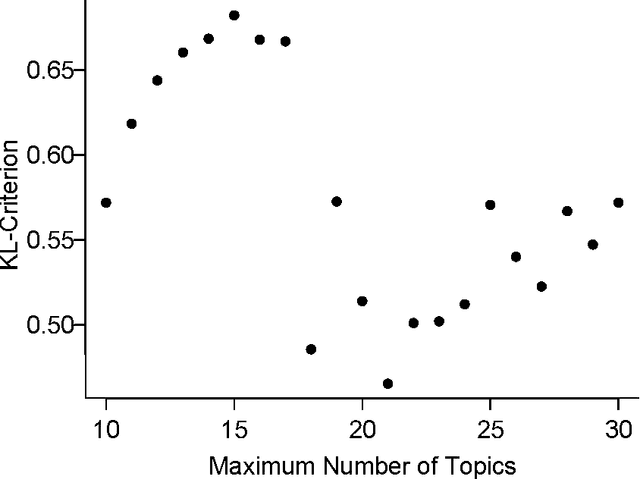
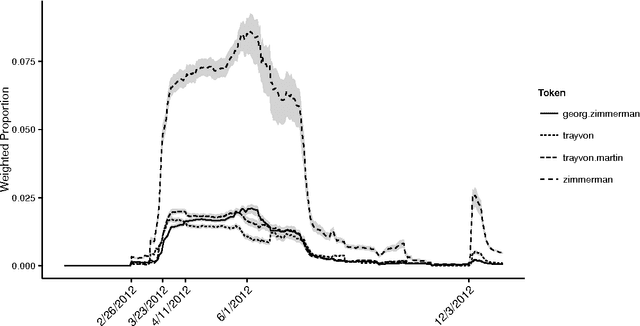
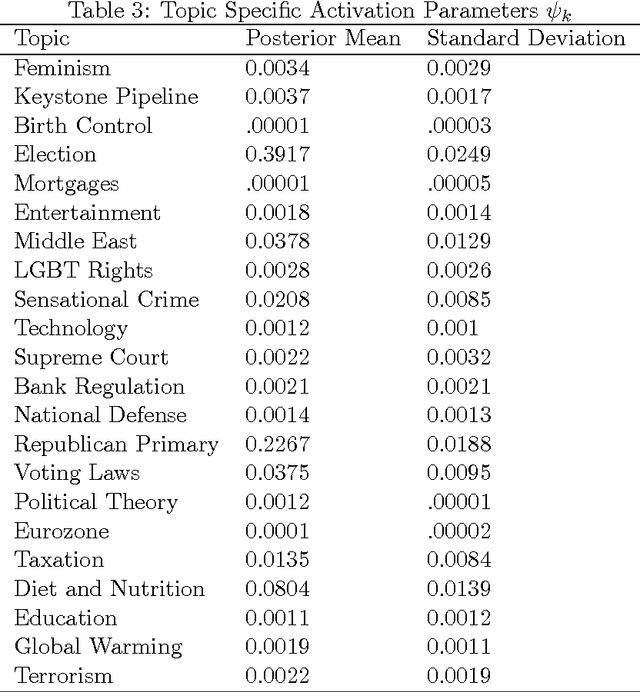
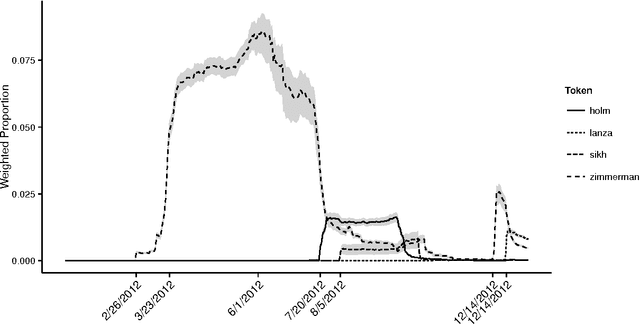
The last decade has seen great progress in both dynamic network modeling and topic modeling. This paper draws upon both areas to create a Bayesian method that allows topic discovery to inform the latent network model and the network structure to facilitate topic identification. We apply this method to the 467 top political blogs of 2012. Our results find complex community structure within this set of blogs, where community membership depends strongly upon the set of topics in which the blogger is interested.