Characterizing the load profile in power grids by Koopman mode decomposition of interconnected dynamics

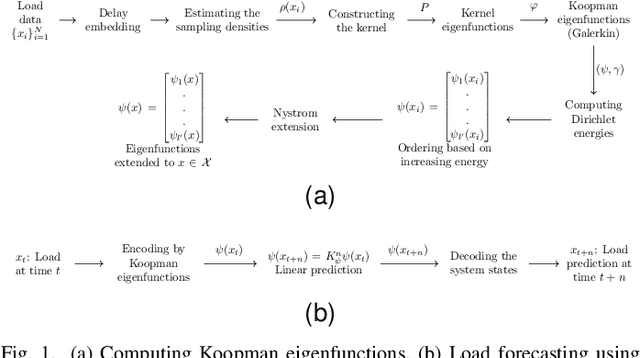
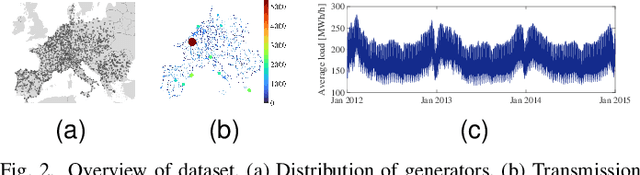
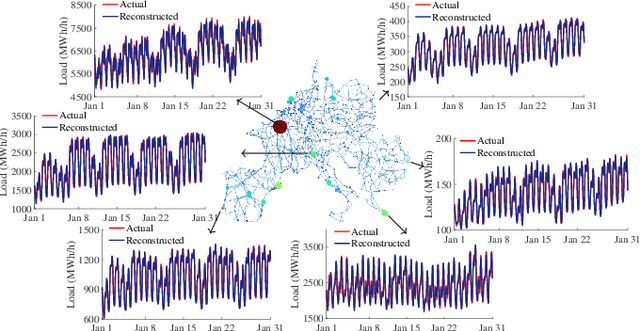
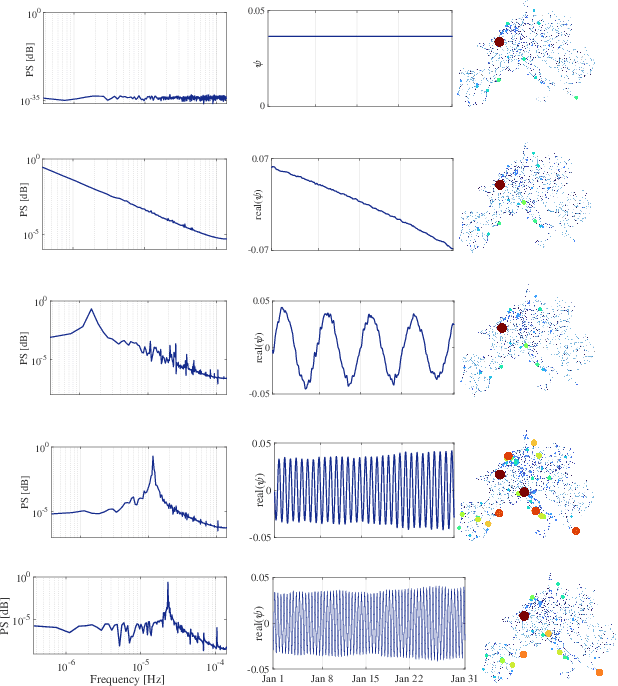
Electricity load forecasting is crucial for effectively managing and optimizing power grids. Over the past few decades, various statistical and deep learning approaches have been used to develop load forecasting models. This paper presents an interpretable machine learning approach that identifies load dynamics using data-driven methods within an operator-theoretic framework. We represent the load data using the Koopman operator, which is inherent to the underlying dynamics. By computing the corresponding eigenfunctions, we decompose the load dynamics into coherent spatiotemporal patterns that are the most robust features of the dynamics. Each pattern evolves independently according to its single frequency, making its predictability based on linear dynamics. We emphasize that the load dynamics are constructed based on coherent spatiotemporal patterns that are intrinsic to the dynamics and are capable of encoding rich dynamical features at multiple time scales. These features are related to complex interactions over interconnected power grids and different exogenous effects. To implement the Koopman operator approach more efficiently, we cluster the load data using a modern kernel-based clustering approach and identify power stations with similar load patterns, particularly those with synchronized dynamics. We evaluate our approach using a large-scale dataset from a renewable electric power system within the continental European electricity system and show that the Koopman-based approach outperforms a deep learning (LSTM) architecture in terms of accuracy and computational efficiency. The code for this paper has been deposited in a GitHub repository, which can be accessed at the following address github.com/Shakeri-Lab/Power-Grids.

A purely data-driven framework for prediction, optimization, and control of networked processes: application to networked SIS epidemic model

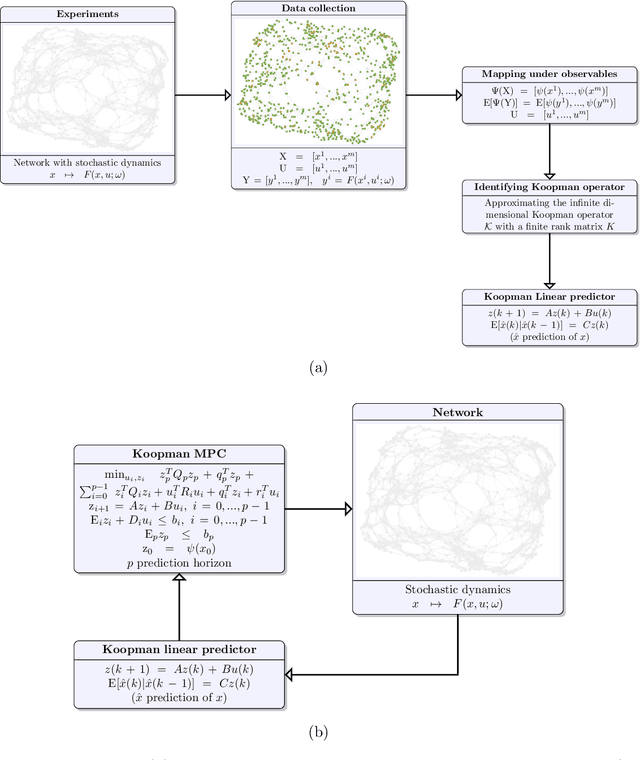
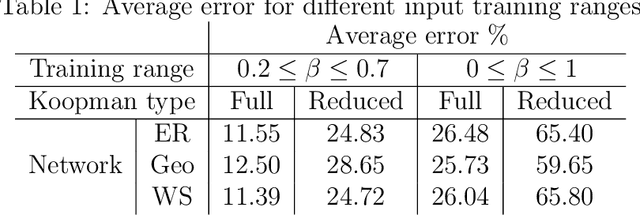
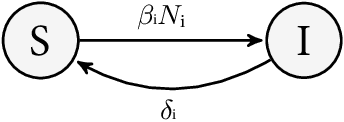
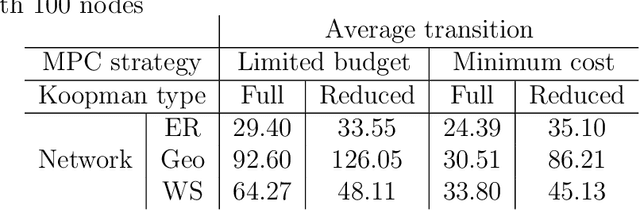
Networks are landmarks of many complex phenomena where interweaving interactions between different agents transform simple local rule-sets into nonlinear emergent behaviors. While some recent studies unveil associations between the network structure and the underlying dynamical process, identifying stochastic nonlinear dynamical processes continues to be an outstanding problem. Here we develop a simple data-driven framework based on operator-theoretic techniques to identify and control stochastic nonlinear dynamics taking place over large-scale networks. The proposed approach requires no prior knowledge of the network structure and identifies the underlying dynamics solely using a collection of two-step snapshots of the states. This data-driven system identification is achieved by using the Koopman operator to find a low dimensional representation of the dynamical patterns that evolve linearly. Further, we use the global linear Koopman model to solve critical control problems by applying to model predictive control (MPC)--typically, a challenging proposition when applied to large networks. We show that our proposed approach tackles this by converting the original nonlinear programming into a more tractable optimization problem that is both convex and with far fewer variables.