Mitigating Exposure Bias in Risk-Aware Time Series Forecasting with Soft Tokens

Autoregressive forecasting is central to predictive control in diabetes and hemodynamic management, where different operating zones carry different clinical risks. Standard models trained with teacher forcing suffer from exposure bias, yielding unstable multi-step forecasts for closed-loop use. We introduce Soft-Token Trajectory Forecasting (SoTra), which propagates continuous probability distributions (``soft tokens'') to mitigate exposure bias and learn calibrated, uncertainty-aware trajectories. A risk-aware decoding module then minimizes expected clinical harm. In glucose forecasting, SoTra reduces average zone-based risk by 18\%; in blood-pressure forecasting, it lowers effective clinical risk by approximately 15\%. These improvements support its use in safety-critical predictive control.

Fusing Biomechanical and Spatio-Temporal Features for Fall Prediction: Characterizing and Mitigating the Simulation-to-Reality Gap

Falls are a leading cause of injury and loss of independence among older adults. Vision-based fall prediction systems offer a non-invasive solution to anticipate falls seconds before impact, but their development is hindered by the scarcity of available fall data. Contributing to these efforts, this study proposes the Biomechanical Spatio-Temporal Graph Convolutional Network (BioST-GCN), a dual-stream model that combines both pose and biomechanical information using a cross-attention fusion mechanism. Our model outperforms the vanilla ST-GCN baseline by 5.32% and 2.91% F1-score on the simulated MCF-UA stunt-actor and MUVIM datasets, respectively. The spatio-temporal attention mechanisms in the ST-GCN stream also provide interpretability by identifying critical joints and temporal phases. However, a critical simulation-reality gap persists. While our model achieves an 89.0% F1-score with full supervision on simulated data, zero-shot generalization to unseen subjects drops to 35.9%. This performance decline is likely due to biases in simulated data, such as `intent-to-fall' cues. For older adults, particularly those with diabetes or frailty, this gap is exacerbated by their unique kinematic profiles. To address this, we propose personalization strategies and advocate for privacy-preserving data pipelines to enable real-world validation. Our findings underscore the urgent need to bridge the gap between simulated and real-world data to develop effective fall prediction systems for vulnerable elderly populations.

Characterizing the load profile in power grids by Koopman mode decomposition of interconnected dynamics

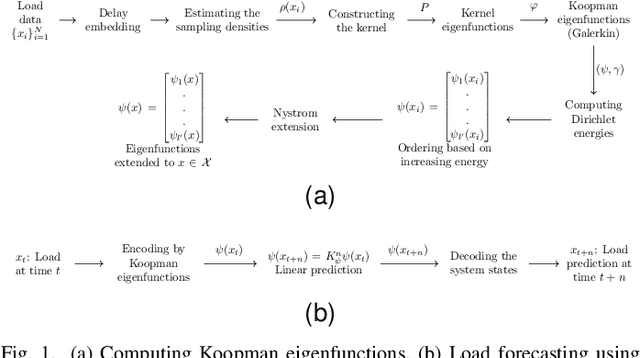
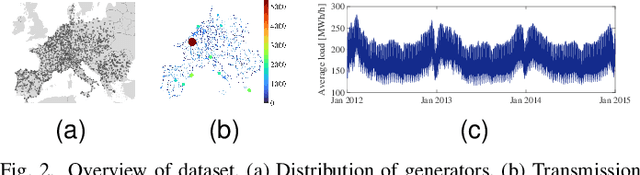
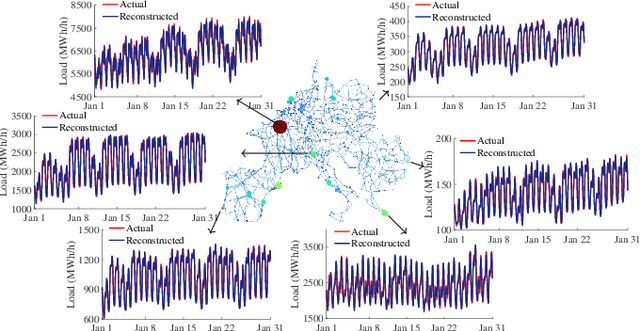
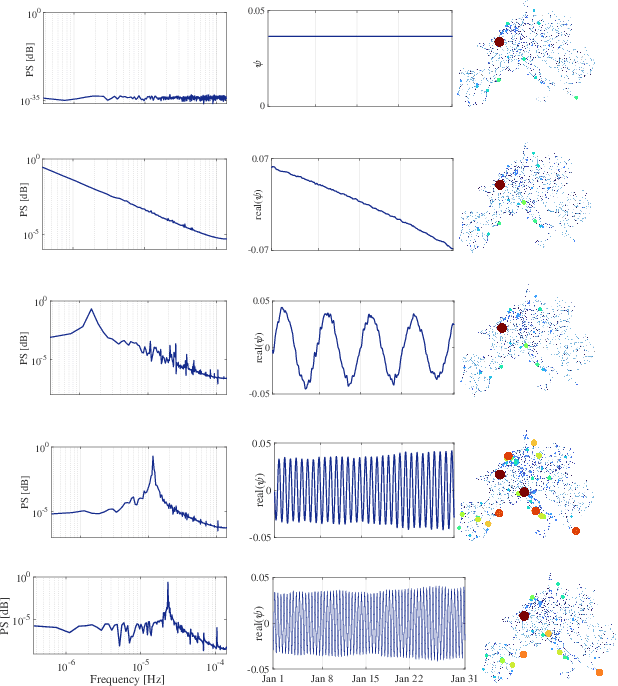
Electricity load forecasting is crucial for effectively managing and optimizing power grids. Over the past few decades, various statistical and deep learning approaches have been used to develop load forecasting models. This paper presents an interpretable machine learning approach that identifies load dynamics using data-driven methods within an operator-theoretic framework. We represent the load data using the Koopman operator, which is inherent to the underlying dynamics. By computing the corresponding eigenfunctions, we decompose the load dynamics into coherent spatiotemporal patterns that are the most robust features of the dynamics. Each pattern evolves independently according to its single frequency, making its predictability based on linear dynamics. We emphasize that the load dynamics are constructed based on coherent spatiotemporal patterns that are intrinsic to the dynamics and are capable of encoding rich dynamical features at multiple time scales. These features are related to complex interactions over interconnected power grids and different exogenous effects. To implement the Koopman operator approach more efficiently, we cluster the load data using a modern kernel-based clustering approach and identify power stations with similar load patterns, particularly those with synchronized dynamics. We evaluate our approach using a large-scale dataset from a renewable electric power system within the continental European electricity system and show that the Koopman-based approach outperforms a deep learning (LSTM) architecture in terms of accuracy and computational efficiency. The code for this paper has been deposited in a GitHub repository, which can be accessed at the following address github.com/Shakeri-Lab/Power-Grids.

Leveraging Wastewater Monitoring for COVID-19 Forecasting in the US: a Deep Learning study

The outburst of COVID-19 in late 2019 was the start of a health crisis that shook the world and took millions of lives in the ensuing years. Many governments and health officials failed to arrest the rapid circulation of infection in their communities. The long incubation period and the large proportion of asymptomatic cases made COVID-19 particularly elusive to track. However, wastewater monitoring soon became a promising data source in addition to conventional indicators such as confirmed daily cases, hospitalizations, and deaths. Despite the consensus on the effectiveness of wastewater viral load data, there is a lack of methodological approaches that leverage viral load to improve COVID-19 forecasting. This paper proposes using deep learning to automatically discover the relationship between daily confirmed cases and viral load data. We trained one Deep Temporal Convolutional Networks (DeepTCN) and one Temporal Fusion Transformer (TFT) model to build a global forecasting model. We supplement the daily confirmed cases with viral loads and other socio-economic factors as covariates to the models. Our results suggest that TFT outperforms DeepTCN and learns a better association between viral load and daily cases. We demonstrated that equipping the models with the viral load improves their forecasting performance significantly. Moreover, viral load is shown to be the second most predictive input, following the containment and health index. Our results reveal the feasibility of training a location-agnostic deep-learning model to capture the dynamics of infection diffusion when wastewater viral load data is provided.

Using Machine Learning to Evaluate Real Estate Prices Using Location Big Data

With everyone trying to enter the real estate market nowadays, knowing the proper valuations for residential and commercial properties has become crucial. Past researchers have been known to utilize static real estate data (e.g. number of beds, baths, square footage) or even a combination of real estate and demographic information to predict property prices. In this investigation, we attempted to improve upon past research. So we decided to explore a unique approach: we wanted to determine if mobile location data could be used to improve the predictive power of popular regression and tree-based models. To prepare our data for our models, we processed the mobility data by attaching it to individual properties from the real estate data that aggregated users within 500 meters of the property for each day of the week. We removed people that lived within 500 meters of each property, so each property's aggregated mobility data only contained non-resident census features. On top of these dynamic census features, we also included static census features, including the number of people in the area, the average proportion of people commuting, and the number of residents in the area. Finally, we tested multiple models to predict real estate prices. Our proposed model is two stacked random forest modules combined using a ridge regression that uses the random forest outputs as predictors. The first random forest model used static features only and the second random forest model used dynamic features only. Comparing our models with and without the dynamic mobile location features concludes the model with dynamic mobile location features achieves 3/% percent lower mean squared error than the same model but without dynamic mobile location features.

A purely data-driven framework for prediction, optimization, and control of networked processes: application to networked SIS epidemic model

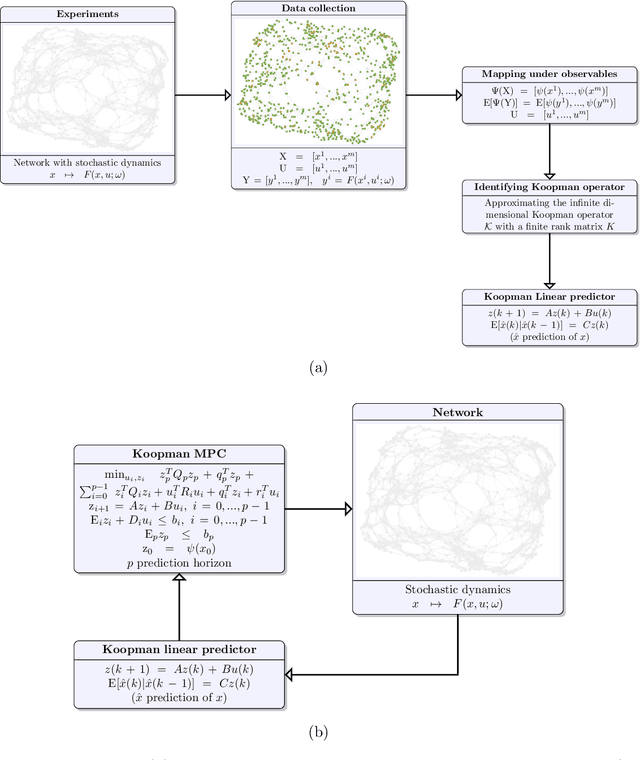
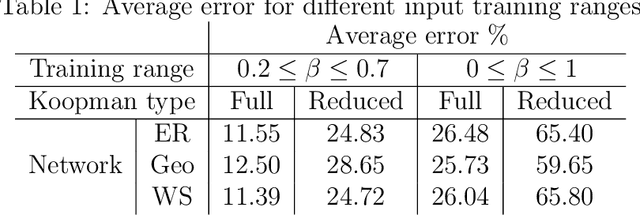
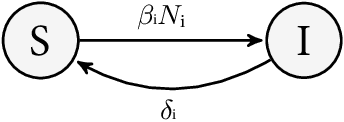
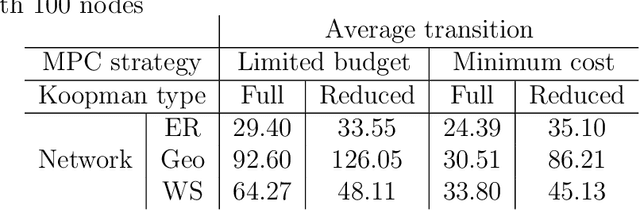
Networks are landmarks of many complex phenomena where interweaving interactions between different agents transform simple local rule-sets into nonlinear emergent behaviors. While some recent studies unveil associations between the network structure and the underlying dynamical process, identifying stochastic nonlinear dynamical processes continues to be an outstanding problem. Here we develop a simple data-driven framework based on operator-theoretic techniques to identify and control stochastic nonlinear dynamics taking place over large-scale networks. The proposed approach requires no prior knowledge of the network structure and identifies the underlying dynamics solely using a collection of two-step snapshots of the states. This data-driven system identification is achieved by using the Koopman operator to find a low dimensional representation of the dynamical patterns that evolve linearly. Further, we use the global linear Koopman model to solve critical control problems by applying to model predictive control (MPC)--typically, a challenging proposition when applied to large networks. We show that our proposed approach tackles this by converting the original nonlinear programming into a more tractable optimization problem that is both convex and with far fewer variables.

A new method for quantifying network cyclic structure to improve community detection

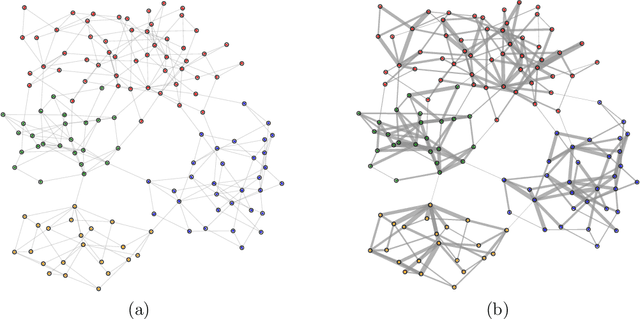
A distinguishing property of communities in networks is that cycles are more prevalent within communities than across communities. Thus, the detection of these communities may be aided through the incorporation of measures of the local "richness" of the cyclic structure. In this paper, we introduce renewal non-backtracking random walks (RNBRW) as a way of quantifying this structure. RNBRW gives a weight to each edge equal to the probability that a non-backtracking random walk completes a cycle with that edge. Hence, edges with larger weights may be thought of as more important to the formation of cycles. Of note, since separate random walks can be performed in parallel, RNBRW weights can be estimated very quickly, even for large graphs. We give simulation results showing that pre-weighting edges through RNBRW may substantially improve the performance of common community detection algorithms. Our results suggest that RNBRW is especially efficient for the challenging case of detecting communities in sparse graphs.