A Dual-mode Local Search Algorithm for Solving the Minimum Dominating Set Problem

Given a graph, the minimum dominating set (MinDS) problem is to identify a smallest set $D$ of vertices such that every vertex not in $D$ is adjacent to at least one vertex in $D$. The MinDS problem is a classic $\mathcal{NP}$-hard problem and has been extensively studied because of its many disparate applications in network analysis. To solve this problem efficiently, many heuristic approaches have been proposed to obtain a good solution within an acceptable time limit. However, existing MinDS heuristic algorithms are always limited by various tie-breaking cases when selecting vertices, which slows down the effectiveness of the algorithms. In this paper, we design an efficient local search algorithm for the MinDS problem, named DmDS -- a dual-mode local search framework that probabilistically chooses between two distinct vertex-swapping schemes. We further address limitations of other algorithms by introducing vertex selection criterion based on the frequency of vertices added to solutions to address tie-breaking cases, and a new strategy to improve the quality of the initial solution via a greedy-based strategy integrated with perturbation. We evaluate DmDS against the state-of-the-art algorithms on seven datasets, consisting of 346 instances (or families) with up to tens of millions of vertices. Experimental results show that DmDS obtains the best performance in accuracy for almost all instances and finds much better solutions than state-of-the-art MinDS algorithms on a broad range of large real-world graphs.

Improved Exact and Heuristic Algorithms for Maximum Weight Clique

We propose improved exact and heuristic algorithms for solving the maximum weight clique problem, a well-known problem in graph theory with many applications. Our algorithms interleave successful techniques from related work with novel data reduction rules that use local graph structure to identify and remove vertices and edges while retaining the optimal solution. We evaluate our algorithms on a range of synthetic and real-world graphs, and find that they outperform the current state of the art on most inputs. Our data reductions always produce smaller reduced graphs than existing data reductions alone. As a result, our exact algorithm, MWCRedu, finds solutions orders of magnitude faster on naturally weighted, medium-sized map labeling graphs and random hyperbolic graphs. Our heuristic algorithm, MWCPeel, outperforms its competitors on these instances, but is slightly less effective on extremely dense or large instances.

Boosting Data Reduction for the Maximum Weight Independent Set Problem Using Increasing Transformations

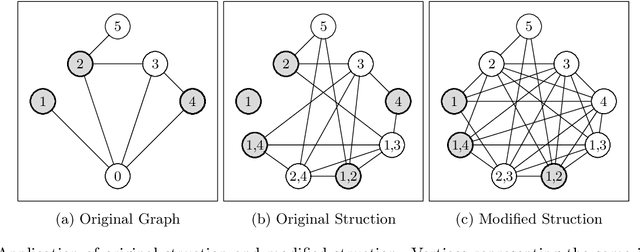
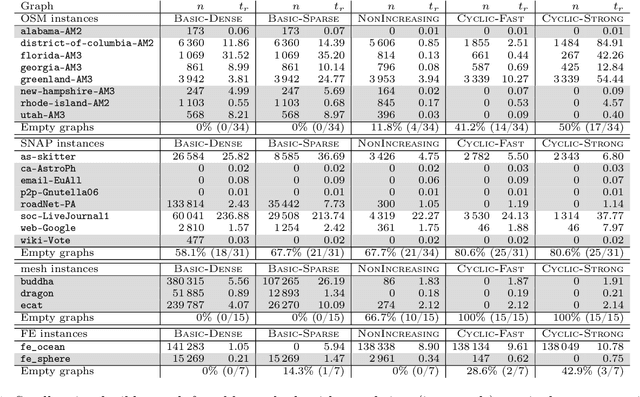
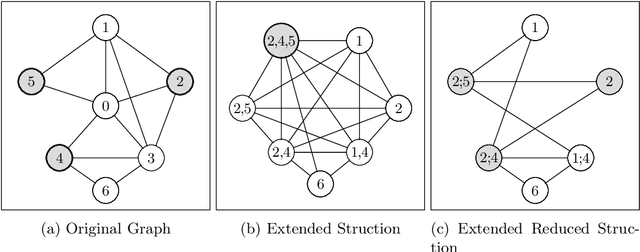
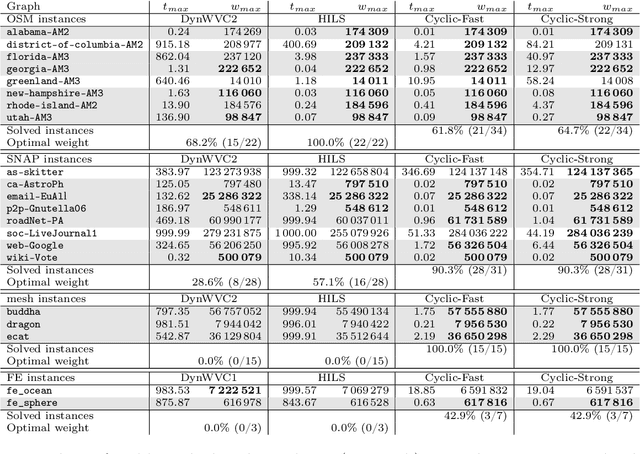
Given a vertex-weighted graph, the maximum weight independent set problem asks for a pair-wise non-adjacent set of vertices such that the sum of their weights is maximum. The branch-and-reduce paradigm is the de facto standard approach to solve the problem to optimality in practice. In this paradigm, data reduction rules are applied to decrease the problem size. These data reduction rules ensure that given an optimum solution on the new (smaller) input, one can quickly construct an optimum solution on the original input. We introduce new generalized data reduction and transformation rules for the problem. A key feature of our work is that some transformation rules can increase the size of the input. Surprisingly, these so-called increasing transformations can simplify the problem and also open up the reduction space to yield even smaller irreducible graphs later throughout the algorithm. In experiments, our algorithm computes significantly smaller irreducible graphs on all except one instance, solves more instances to optimality than previously possible, is up to two orders of magnitude faster than the best state-of-the-art solver, and finds higher-quality solutions than heuristic solvers DynWVC and HILS on many instances. While the increasing transformations are only efficient enough for preprocessing at this time, we see this as a critical initial step towards a new branch-and-transform paradigm.

Distributed Evolutionary k-way Node Separators

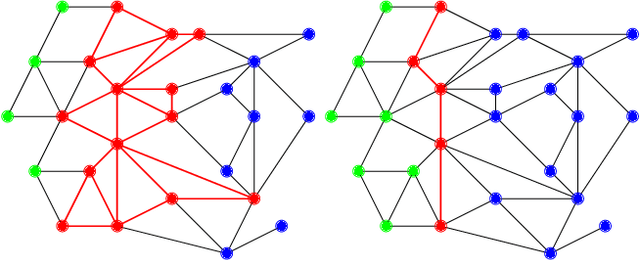
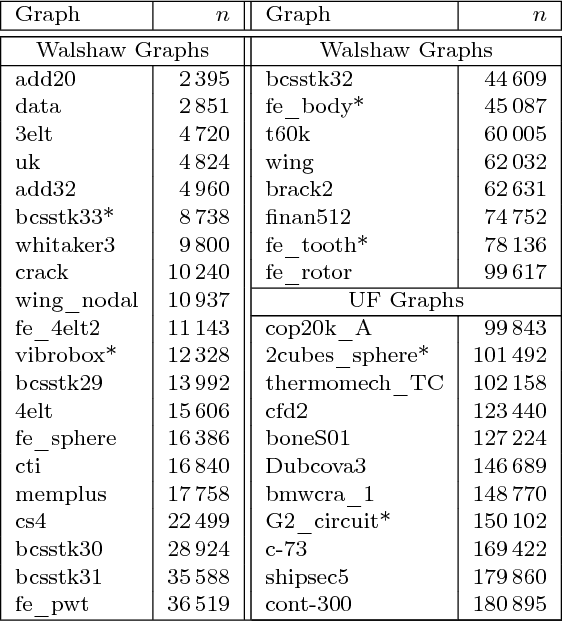
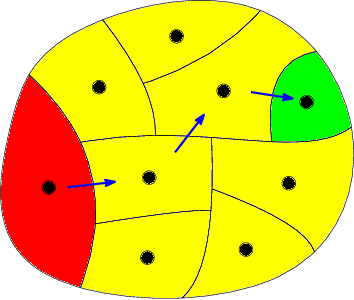
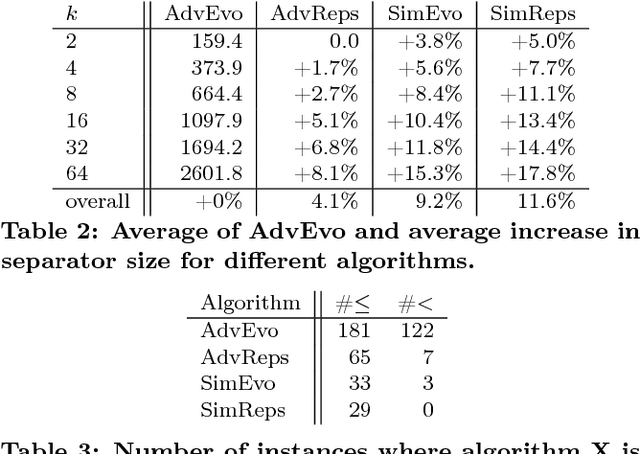
Computing high quality node separators in large graphs is necessary for a variety of applications, ranging from divide-and-conquer algorithms to VLSI design. In this work, we present a novel distributed evolutionary algorithm tackling the k-way node separator problem. A key component of our contribution includes new k-way local search algorithms based on maximum flows. We combine our local search with a multilevel approach to compute an initial population for our evolutionary algorithm, and further show how to modify the coarsening stage of our multilevel algorithm to create effective combine and mutation operations. Lastly, we combine these techniques with a scalable communication protocol, producing a system that is able to compute high quality solutions in a short amount of time. Our experiments against competing algorithms show that our advanced evolutionary algorithm computes the best result on 94% of the chosen benchmark instances.

Finding Near-Optimal Independent Sets at Scale

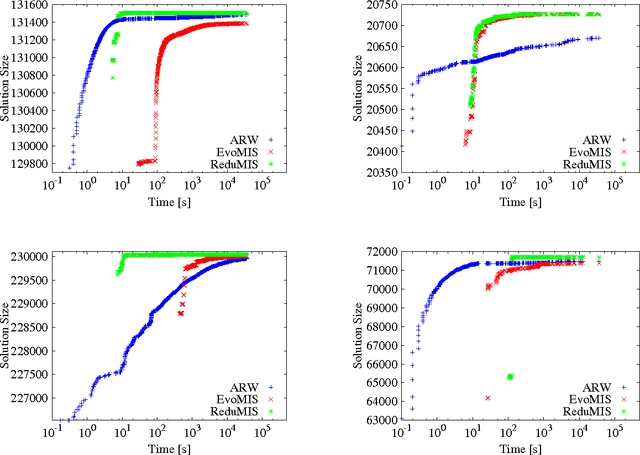
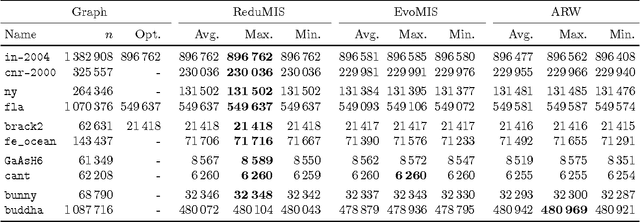
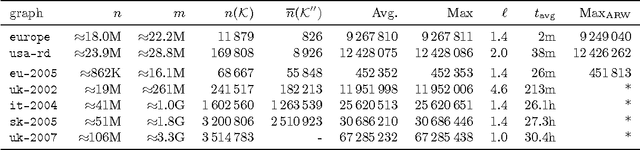
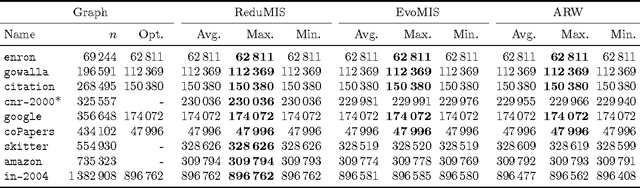
The independent set problem is NP-hard and particularly difficult to solve in large sparse graphs. In this work, we develop an advanced evolutionary algorithm, which incorporates kernelization techniques to compute large independent sets in huge sparse networks. A recent exact algorithm has shown that large networks can be solved exactly by employing a branch-and-reduce technique that recursively kernelizes the graph and performs branching. However, one major drawback of their algorithm is that, for huge graphs, branching still can take exponential time. To avoid this problem, we recursively choose vertices that are likely to be in a large independent set (using an evolutionary approach), then further kernelize the graph. We show that identifying and removing vertices likely to be in large independent sets opens up the reduction space---which not only speeds up the computation of large independent sets drastically, but also enables us to compute high-quality independent sets on much larger instances than previously reported in the literature.