Finding Near-Optimal Independent Sets at Scale
Paper and Code
Sep 02, 2015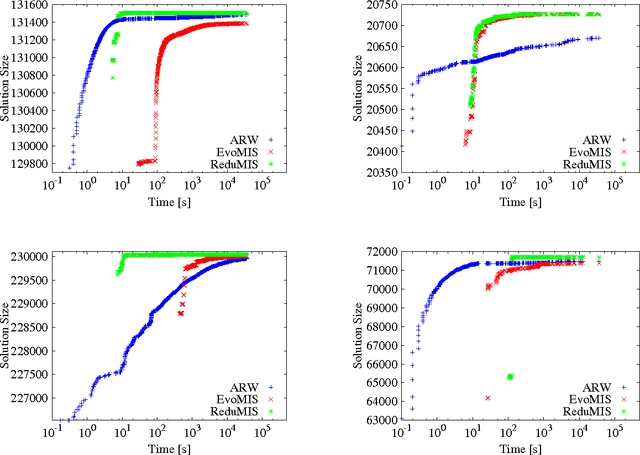
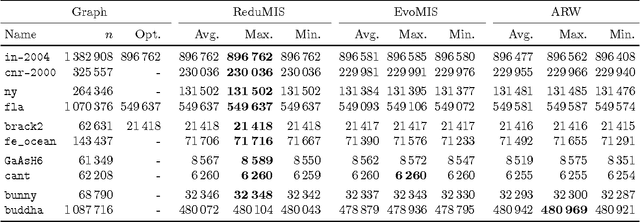
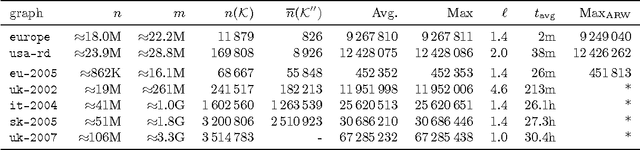
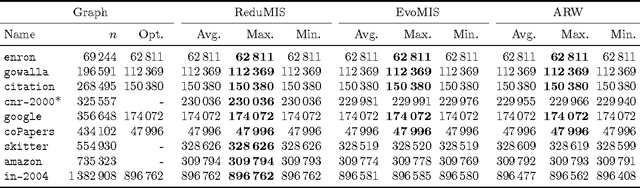
The independent set problem is NP-hard and particularly difficult to solve in large sparse graphs. In this work, we develop an advanced evolutionary algorithm, which incorporates kernelization techniques to compute large independent sets in huge sparse networks. A recent exact algorithm has shown that large networks can be solved exactly by employing a branch-and-reduce technique that recursively kernelizes the graph and performs branching. However, one major drawback of their algorithm is that, for huge graphs, branching still can take exponential time. To avoid this problem, we recursively choose vertices that are likely to be in a large independent set (using an evolutionary approach), then further kernelize the graph. We show that identifying and removing vertices likely to be in large independent sets opens up the reduction space---which not only speeds up the computation of large independent sets drastically, but also enables us to compute high-quality independent sets on much larger instances than previously reported in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge